Monotone Convergence Theorem: Examples, Proof

Sequence and Series >

Not all bounded sequences converge, but if a bounded a sequence is also monotone (i.e. if it is either increasing or decreasing), then it converges. This fact, that every bounded monotone sequence converges is called the monotone convergence theorem [1].

For example, the sequence a_n = 2 -(4/n) converges by the theorem as it is both bounded above and monotone:

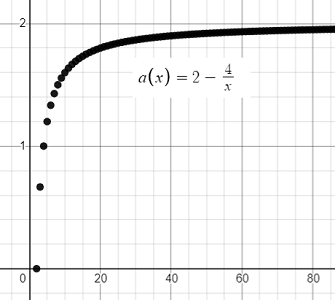
We can prove that a sequence converges using the theorem.

Example question: Prove that the following sequence converges [2]:


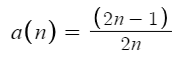
Solution: In order to apply the monotone convergence theorem, we have to show that the sequence is both monotone and bounded:

• The sequence is monotone decreasing because a_{n + 1} < a_n
• The sequence is bounded below by zero (you can deduce this because the numerator is always smaller than the denominator, so if you try to head towards zero, you’ll just get smaller and smaller fractions, but they will never go past zero).

Therefore, by the monotone convergence theorem, this sequence converges.

Proof of the Monotone Convergence Theorem

We can use the monotone convergence theorem to prove that bounded monotone sequences converge. But we can also prove the theorem itself. Specifically, we want to prove that the limit of a monotone bounded sequence exists. Several proofs exist, but this version is probably the most concise [3, 4]:

Suppose that a_n is an increasing sequence.

• Define S as the set of terms in a_n (S = a_n: n ∈ ℕ).
• We know that the limit superior L = sup(S) exists via the Completeness Axiom because this is a bounded set.
• Let ε > 0.
• Then L – ε is not an upper bound for S; by the definition of supremum (i.e. L is the least upper bound). Therefore, there must be a number N such that a_N L – ε.
• Since a_n is increasing for all n ≥ N, it follows that a_n > L – ε.
• since L is an upper bound, we know that a_n ≤ L < L + ε.
• From the above, we can conclude that for all n ≥ N: L – ε < a_n < L + ε and so |a_n – L| < ε.

References

[1] Bakker, L. Math 341 Lecture #8 §2.4: The Monotone Convergence Theorem and a First Look at Infinite Series. Retrieved May 6, 2021 from: https://math.byu.edu/~bakker/M341/Lectures/Lec09.pdf
[2] Romik, D. (2011). Math 25 — Solutions to Homework Assignment #7. UC Davis, Spring 2011. Retrieved May 6, 2021 from: https://www.math.ucdavis.edu/~romik/teaching-pages/mat25-hw7solns.pdf
[3] More concise proof of part (a) of the monotone convergence theorem. Math 0450
Honors intro to analysis Spring, 2009. Retrieved May 6, 2021 from: http://www.math.pitt.edu/~sph/0450/0450-notes12.pdf
[4] Math 410 Section 2.3: The Monotone Convergence Theorem. Retrieved May 6, 2021 from: http://www.math.umd.edu/~immortal/MATH410/lecturenotes/ch2-3.pdf