Estimators > German Tank Problem
German Tank Problem
The German Tank Problem is a way to estimate the total population size from a small sample. It’s commonly used in AP statistics to teach about estimators. The problem was originally developed by the Allies during World War II, when it was used to estimate the total number of German tanks from a small number of serial numbers from captured, destroyed, or observed tanks. It was extended to estimate the number of factories and other manufactured parts. Today, the formula has been applied for wide reaching applications like estimating the number of iPhones sold.
The idea is that tanks were numbered 1,2,…x, where “x” was the unknown total number of tanks. If we know just a few tank numbers, we can use them to estimate x.
Formula
The formula to solve the German Tank problem is:
Where:
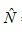= population maximum,- m = sample maximum (i.e. the highest serial number),
- n = sample size.
Example
Example problem: You capture 5 enemy tanks with serial numbers 1, 31, 43, 79, and 115. What is the likely population maximum?
Solution:
Step 1: Insert the given values into the formula. For this example, the sample size is 5 and the highest value in the sample is 115, so:
= 115 + (115 / 5) – 1
Step 2: Solve:
= 115 + (115 / 5) – 1
= 115 + 23 – 1
= 138 – 1
= 137
The population maximum is 137.
The History Behind the Problem
In World War II, the Allies did not know how many tanks the Germans were making. After a set of German Mark V tanks were captured and statisticians theorized (correctly) that the Germans numbered those tanks sequentially as they came off the production line. The statisticians used the above formula to estimate that 246 tanks were being made per month between June 1940 and September 1942; This was a significant reduction from intelligence estimates which put the number at about 1400. After the war, the Allies inspected the German’s production records and found that the true number of tanks produced per month was 245 — extremely close to the statisticians’ estimate.
Minimum Variance Unbiased Estimator
The solution to the tank problem is an example of a Minimum Variance Unbiased Estimator (MVUE). An unbiased estimator is an accurate statistic that’s used to approximate a population parameter; “Minimum Variance” means that out of all of the possible estimates, the formula:
is the one with the lowest variance. “Possible estimates” include every way you can think of that could estimate the total number of tanks. As well as the above formula, your guesstimates might include:
- Doubling the sample mean.
- Multiplying the sample standard deviation by five.
- Ass the sample maximum plus the sample minimum.
And so on. The MVUE will be the formula with the lowest variance. In other words, the formula m + (m/n) + 1 gives a result that’s closer to the mean than any of the other potential formulas.
References:
Davies, G. 2006. Gavyn Davies Does the Maths; How a Statistical Formula Won the War. The Guardian. 19 July 2006. Retrieved November 14, 2016. Available online here.