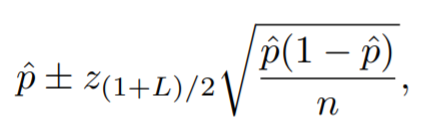Wald CI

The Wald CI, also called the Wald interval or Classical Large-Sample Interval, is a common method to find binomial confidence intervals. It is named after Romanian mathematician Abraham Wald.

Wald CI Formula

The formula is [1]:

Where:

n = sample size,
p-hat = sample proportion,
z_(1+L)/2 = (1+L)/2 standard normal distribution quantile.

Disadvantages

The Wald CI doesn’t perform well for small samples or when proportions are close to 0 or 1. Wald intervals are based on the normal approximation to the binomial distribution. This means that Wald intervals are not suitable for small sample sizes, as they tend to be liberal — meaning that their advertised coverage is lower than the actual interval. For example, when successes are not near 50%m its average coverage is around 60%, not 95% [2].

Therefore, the Wald CI should only be used for larger samples. How large? The performance of the formula relies not only on the sample size, but the unknown population proportion. Many textbook state the “magic number” is a sample size > 10, but this should be used with caution. Adjusted Wald Confidence intervals may help with small samples (for example, see [2]).

Using a Wald CI to test a hypothesis about a population proportion may increase in Type I or Type II errors; you may be able avoid this possibility by using the hypothesized value, p₀, to calculate the standard error instead of the sample proportion [3].

Although easy to compute, the inherent problems with Wald CI coverages have led to some authors discouraging use of the CI except for sample size planning [4]. Two alternatives are the Clopper-Pearson “Exact” Method or the score interval. However, both of these are usually presented in advanced mathematical texts and are challenging to calculate [5].

References

[1] Confidence Intervals for a Single Population Proportion.
[2] Agresti, A. and Coull, B. (1998). Approximate Is Better than “Exact” for Interval Estimation of Binomial Proportions.
[3] Yang, S. & Black, K. (2019). Using the Standard Wald Confidence Interval for a Population Proportion Hypothesis Test is a Common Mistake. In Teaching Statistics. Volume 41, Number 2.
[4] McGrath, O. & Burke, K. (2021. Binomial confidence intervals for rare events:
importance of defining margin of error relative to
magnitude of proportion. Retrieved February 6, 2021 from: https://arxiv.org/pdf/2109.02516.pdf
[5] Sauro, J. & Lewis, J. ESTIMATING COMPLETION RATES FROM SMALL SAMPLES USING BINOMIAL CONFIDENCE INTERVALS: COMPARISONS AND RECOMMENDATIONS. PROCEEDINGS of the HUMAN FACTORS AND ERGONOMICS SOCIETY 49th ANNUAL MEETING—2005 2100