In statistics, the term “score interval” has two completely different meanings. It can refer to either:
- Score intervals on frequency distributions, or
- The Wilson technique to calculate confidence intervals.
Definition 1: Score Intervals on Frequency Distributions
A score interval is a range of possible scores on a frequency distribution or histogram [1]. For example, the following frequency histogram shows books and the number of books sold:
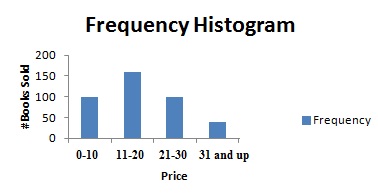
Each score interval on this histogram is represented by a blue bar: 0 to 10, 11 to 20, 21 to 30, and 31 and up.
Definition 2: The Wilson Score Interval
The Wilson Score interval, developed by Edwin Wilson in 1927 [2], is an improvement of the Wald CI, to accommodate for loss of coverage seen with small samples. The idea is that you use an observed value for the population proportion, p, instead of an expected probability, P. The technique also works well for skewed distributions, where p might be close to 0 or 1.
The improvement is so marked, it’s recommended that you always use the score interval instead of the Wald when dealing with small samples. Wilson’s original formula is complex and usually performed with a computer. The endpoints for a Wilson score interval are given by the formula a ± z(1+L)/2b, where a and
b are given by [3]:
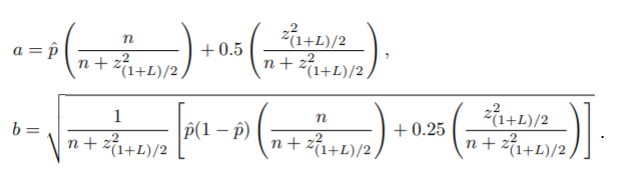
However, you can get a good approximation with the following procedure:
Step 1: Calculate adjusted y with the formula (y is the number of observed successes in the sample):
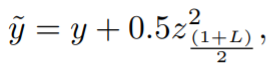
Step 2: Calculate adjusted n with the formula:
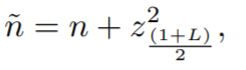
Step 3: Calculate adjusted p with the formula:
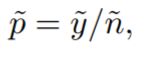
Step 3: Substitute adjusted p and n from Steps 2, and 3, into the Wald confidence interval formula:
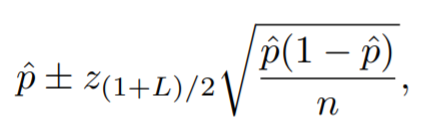
Giving:
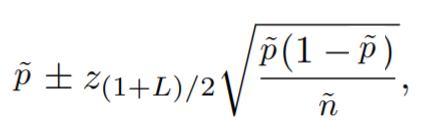
References
[1] Phillips, J. (1999). How to Think About Statistics. Sixth Edition. Henry Holt and Company.
[2] Wilson, E.B. 1927. Probable inference, the law of succession, and statistical inference. Journal of the American Statistical Association 22: 209-212. PDF.
[3] Confidence Intervals for a Single Population Proportion. Retrieved February 6, 2021 from: http://www.math.wpi.edu/Course_Materials/SAS/new_bici.pdf