Binomial Confidence Interval

Binomial Theorem >

You may want to read these articles first:
What is a Confidence Interval?
What is a Binomial Distribution?

What is a Binomial Confidence Interval?

The binomial confidence interval is a measure of uncertainty for a proportion in a statistical population. It takes a proportion from a sample and adjusts for sampling error.

Let’s say you needed a 100(1-α) confidence interval (where α is the significance level) on a certain parameter p for a binomial distribution. Exactly how you would achieve this depends on the values for n (your sample size) and p:

1. Large sample size (> 15) and large p (≥ 0.1): The normal approximation method works well (Herson, 2009) unless the proportion is close to 0 or 1 (Razdolsky, 2014). The general rule of thumb is that you can use the normal approximation when n * p and n * q (q is just 1 – p) are greater than 5. For more on this, see: Using the normal approximation to solve a binomial distribution problem.
2. Large sample size (> 15) and small p (< 0.1): The Poisson approximation for the binomial is a better choice (Montgomery, 2001).
3. Small samples (15 or under): a binomial table should be used to find the binomial confidence interval for p.

All of the formulas associated with a binomial confidence interval work on the assumption of an underlying binomial distribution. In other words, your experiment has a fixed number of trials with two outcomes, a “success” or “failure.” Success and failure are generic terms for two opposing outcomes, which could be yes/no, black/white, voted/didn’t vote, or a myriad of other options,

1. Large N, Large P (Normal Approximation)

For large samples, you can approximate the binomial using a normal distribution. This is justified by the Central Limit Theorem.

One Sample

The formula for the CI on parameter p is:



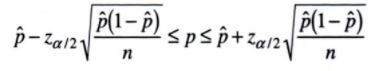
The unbiased point estimator, p is the proportion of “successes” in a Bernoulli trial. As a formula, that’s:



Z alpha/2 is an alpha level’s z-score for a two tailed test. See: What is Z Alpha/2?

Two Sample

The formula for the difference on p₁ – p₂ is:

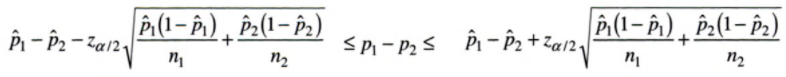
2. Approximating using the Poisson Distribution

You have a couple of choices here. The first is to use one of the many calculators available online. A good one is this one, which gives you values for a 95% CI. The second option is to use a table, such as the one at the bottom of this article: Table for 95% exact confidence intervals for the Poisson Distribution.
Let’s use an example to show how the table works. You have a small sample of observations (n = 6) from a total population of 10,000. For this low level of occurrence in the population, the Poisson gives a good approximation to the binomial. To find the mean(μ) and the associated confidence interval:

1. Locate the 95% low and high values in the table for 95% exact confidence intervals for the Poisson Distribution.. For n = 6, the low is 2.202 and the high is 13.06.
2. Divide the numbers you found in the table by the number of population members. In this example, there are 10,000 members, so the confidence interval is:
   • 2.202 / 10,000 = 0.00022
   • 13.06 / 10,000 = 0.001306

Exact 95% CI Table for the Poisson Distribution

The following table shows the first few values for an exact 95% confidence limit for the Poisson Distribution (adapted from Appendix 1 of Ahlbom’s Biostatistics for Engineers):

# Observed Events	95% Low	95% High
0	0.000	3.689
1	0.025	5.572
2	0.242	7.225
3	0.619	8.767
4	1.090	10.24
5	1.623	11.67
6	2.202	13.06
7	2.814	14.42
8	3.454	15.76
7	2.814	14.42
8	3.454	15.76
9	4.115	17.09
10	4.795	18.39
11	5.491	19.68
12	6.201	20.96
13	6.922	22.23
14	7.654	23.49
15	8.395	24.74
16	9.145	25.98
17	9.903	27.22
18	10.67	28.45
19	11.44	29.67
20	12.22	30.89

References

Herson, J. (2009). Data and Safety Monitoring Committees in Clinical Trials. CRC Press.
Montgomery, D. (2001). Introduction to Statistical Quality Control. 4th Edition. Wiley & Sons.
Radolsky, L. (2014). Probability-Based Structural Fire Load. Cambridge University Press.