Statistics Definitions > W Statistic (Coefficient of Concordance)
This article is about Kendall’s W Statistic for ranked data.
- For the W-value given to indicate normalilty, see: Shapiro-Wilk Test.
- For the “W-statistic” used in ANOVA, see: Brown-Forsythe test.
What is the W Statistic?
Kendall’s W statistic (sometimes called the Coefficient of Concordance) is a non parametric statistic used to assess agreement between different raters, and ranges from 0 to 1. Zero is no agreement at all between raters, while 1 is perfect agreement. The statistic is calculated either on an interval scale or on an ordinal scale.
For example, let’s say a group of workers were asked to rank a list of workplace concerns from least important to most important.
- If the W Statistic is 0, that means everyone ranked the list differently (or randomly).
- If the W Statistic is 1, then everyone ranked the list in exactly the same order.
Caution: you should only use the W statistic for measuring concordance between variables that are measuring the same general properties of objects. For example, if negative and positive correlations are of equal importance, this would not be a suitable test.
W is the notation used if the statistic is from a population. W̄ is the notation for the sample statistic.
Formula
The formula for the W statistic is:
![]()
Where:
- S is the sum of squared deviations,
- m is the number of judges (raters),
- n is the total number of objects being ranked.
A Second formula can also be used that gives the same results, where T is a correction factor for tied ranks:
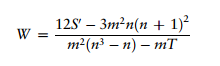 .
.
In theory, Kendall’s W can be used for 2 judges. However, Cohen’s Kappa or Spearman’s Rank Correlation Coefficient are better choices in this case.
According to Pierre Legendre, the term “judges” is usually only used in the social sciences. But Kendall’s W isn’t restricted to situations in the social sciences where people rank a list of items. For example, judges could be:
- Species (in community ecology), where population size can be used to evaluate habitat quality.
- Characteristics of different species, individuals, or populations (in taxonomy).
Reference:
Legendre, P. 2010. Coefficient of Concordance. Pp. 164-169 in: Encyclopedia of Research Design, Vol 1. NJ Salkind ed. SAGE Publications Inc.