A closed surface contains a volume of space, enclosed from all directions; It consists of one connected, hollow piece that has no holes and doesn’t intersect itself.
A closed surface has a natural positive direction, where a unit normal vector N points away from the interior (i.e. points toward the outside). A normal vector pointed outward indicates the “negative” direction.
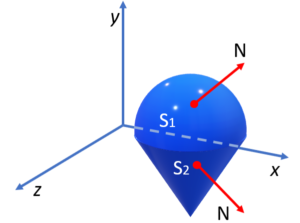
Closed Surface Examples

Examples of closed surfaces:
- Cube,
- Polyhedron,
- Sphere,
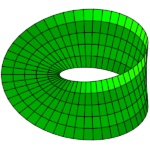
- Torus (an inflated inner tube).
- Gaussian surface: any closed surface through which an electric field passes [1].
A Few examples of surfaces that are not closed: a plane, a sphere with a point removed, a crumpled tin can with a cross-section that looks like a figure-8 (it intersects itself), an infinite cylinder [2].
Do Closed Surfaces have a Boundary?
Calculating Integrals
When you have many surfaces (for example, a pyramid has four), calculating integrals becomes a challenge. The divergence theorem allows you to combine multiple surface integrals and use one triple (volume) integral instead.
References
[1] Chapter 24 Lecture. Retrieved April 22, 2021 from: http://www.physics.gsu.edu/dhamala/Phys2212/chap24.pdf
[2] MIT. (2007). 18.02 Multivariable Calculus. Retrieved April 22, 2021 from: https://ocw.mit.edu/courses/mathematics/18-02-multivariable-calculus-fall-2007/readings/divergance_thm.pdf. CC Share Alike 4.0.
[3] Lntcnnmc, CC BY-SA 3.0
[4] V9. Surface Integrals. Retrieved April 22, 2021 from: http://math.mit.edu/~jorloff/suppnotes/suppnotes02/v9.pdf
[5] Classification of Surfaces. Retrieved April 22, 2021 from: https://people.math.osu.edu/fiedorowicz.1/math655/classification.html