A unit normal vector gives the orientation of a surface; It is a vector with a length of one that is perpendicular to a surface. It gets its name because it is part unit vector and part normal vector. Any nonzero vector can be divided by length to get a unit vector, much in the same way a real number can be divided by itself to get 1. The normal vector can also be divided by its length to get a unit normal vector [1]. The simplest way to find the unit normal vector n̂(t) is to divide each component in the normal vector by its absolute magnitude (size). For example, if a vector v = (2, 4) has a magnitude of 2, then the unit vector has a magnitude of: Note: Magnitude is another name for “size”. You can figure out the magnitude of any number by removing the negative sign — giving you the absolute value. For example, the absolute value of -100 is 100, which is also the magnitude. Scalar variables have magnitude or a numerical value, and not direction. Vectors have magnitude and direction.) Another way is with the following formula: This is sometimes called the principal unit normal vector [2]. For a curve, the unit tangent vector and unit normal vector are orthogonal (at right angles) to each other. While unit tangent vectors “fly off” a curve like a roller coaster car off its tracks, unit normal vectors always point to the “inside” of a curve: [1] Dot Product and Normals to Lines and Planes. Retrieved April 22, 2021 from: https://sites.math.washington.edu/~king/coursedir/m445w04/notes/vector/normals-planes.html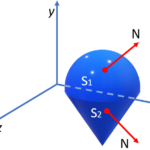
Constructing a Unit Normal Vector
v = (2/2, 4/2) = (1, 2).
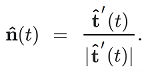
Where:
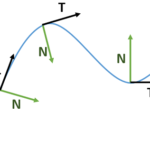
If you can imagine that the above graph is a roller coaster, the unit normal vector is pointing in the direction of the forces pulling the “car”; This is one useful application of unit normals: they point roughly in the direction of forces pulling the “point” or particle; In a sense, they “point the way.”References
[2] Abstract. We introduce two important unit vectors.
https://ximera.osu.edu/mooculus/calculus3/master/normalVectors/digInUnitTangentAndUnitNormalVectors
Unit Normal Vector
Comments? Need to post a correction? Please Contact Us.