A linear term has a degree of 1. For example, 5x, -2x and x are all linear terms. These terms are x to the first degree (X1), where the “1” isn’t written (because any number to the first power is just that number).
Terms that are not linear are called non-linear terms. The most common one you’ll come across in calculus is the quadratic term.
Quadratic Term, Linear Term and Constant Term
Watch the video for an overview, or read on below:
A quadratic equation has the form f(x) = ax2 + bx + c, which contains three terms:
- ax2 = the quadratic term,
- bx = the linear term,
- c = the constant term.
For example, for the function f(x) = 9x2 + 3x – 5, the linear term is 3x.
Not all quadratic functions have linear terms. For example, 10x2 – 5 = 0.
Coefficient of Linear Terms
The “3” in the above equation is the coefficient , and the “x” is the variable.
It’s possible to have more than one coefficient of a linear term. For example, the coefficient here:
f(x) = 9x2 + 3bx – 5
is 3b.
How It Affects the Shape of Parabolas
Changing the linear term affects the vertex position, both horizontally (along the x-axis) and vertically (along the y-axis).
Increasing “b” moves the parabola down and to the left:
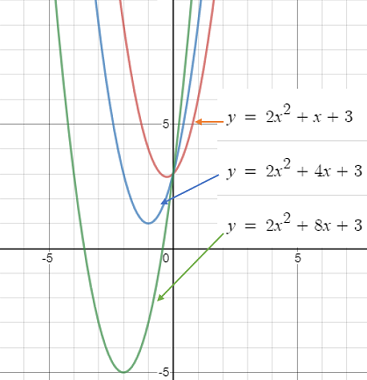
Decreasing “b” moves the parabola down and to the right:
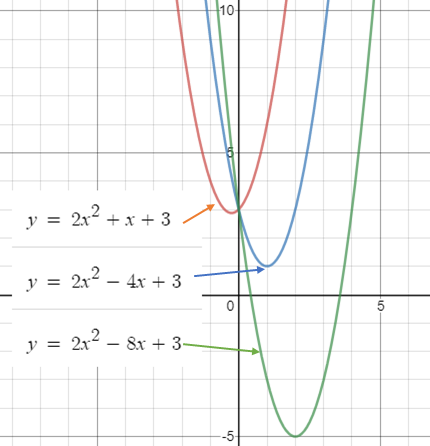
This may come as a surprise: decreasing “b” moves the graph towards the positive direction on the x-axis, and increasing it will move it in the negative x-direction.
References
Graphing calculator on Desmos.
Quadratic Functions. Retrieved November 5, 2019 from: https://math.dartmouth.edu/opencalc2/cole/lecture3.pdf