Polynomial in Standard Form

Standard Form >

A polynomial in standard form is written with the terms in order from highest degree, to lowest degree. For example, the polynomial 4x³ + 8x² + 2x – 21 can be written in standard form as:

Generally, speaking, the standard form of a polynomial equation can be written as:

In other words, set your polynomial equal to 0 and write the terms in descending order by degrees. Sometimes (depending on your professor) it’s okay to omit the “= 0” part of the equation. Usually the clue is in the wording of the question:

• If you are giving an equation already set equal to zero, then include “= 0” in your answer.
• If you are given an equation that doesn’t include “= 0”, it’s usually okay to omit it.

For example, 5 + 9x³ -2x = 0 written in standard form is
9x³ -2x + 5 = 0.
But p(x) = 5 + 9x³ -2x in standard from is
p(x) = 9x³ -2x + 5.

Polynomial in Standard Form: A Few Rules

The variable x is always assigned a degree of 1 and a constant term is always assigned a degree of zero (the “degree” doesn’t exist for a constant as there is no variable). Degree 0 polynomials are sometimes called constant polynomials [1].

If you have more than one variable in a term, make sure to add all of the degrees up to get the correct degree. For example, 3x⁵ + 5x³y + ⁴y⁵z² is written as a polynomial in standard form as:
⁴y⁵z² + 3x⁵ + 5x³y.

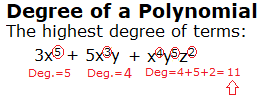
Example question: Which of these polynomials is in standard form?

1. 4 + 5x
2. 5x + 3 – x²
3. -21x⁵ + 3x³ – 99.

Solution: The third expression (-21x⁵ + 3x³ – 99) is in standard form because it is written in order of degree,

Example question #2: Write the following polynomial in standard form and classify the expression by degree: 3x² – 7x4 + 38 + 4x.

Solution:

Step 1: Write the degree of each term:

• 3x² = 2nd degree
• – 7x4 = 4th degree
• + 38 = zero degree
• + 4x = 1st degree.

Step 2: Reorder the terms by order of degree:

– 7x4 + 3x² + 4x + 38.

References

[1] Wortman, K. Polynomials in Two Variables.