Trinomial in Standard Form

Standard Form >

A trinomial is a polynomial expression with three terms. For example:

• 3x – 8 + 4x²
• x² – 2 + 4x
• 10x – 8x³ + 3

How to Write a Trinomial in Standard Form

To write a trinomial in standard form, list the terms in order of degree (the exponent or sum of exponents in each term): highest to lowest, and left to right.

Example 1: write the trinomial 3x – 8 + 4x² in standard form.

Step 1: Note the degree of each term. There are three terms:

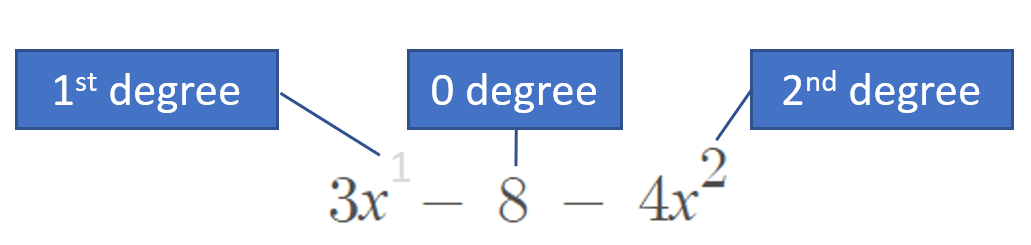
• 3x = Degree of 1; when x is on its own, it’s to the first power but we usually don’t write that out,
• 8 = Degree of zero; constants are usually assigned a zero degree or no degree at all. Another way to think of this: there isn’t a variable there so the degree doesn’t exist and must be zero,
• 4x² = Degree of 2.

Step 2: Write the terms in order of degree (don’t forget to use the correct ± signs from the original expression):
4x² + 3x – 8.

Example 2: Express (x – 5)² as a trinomial in standard form.

Step 1: Write the expression as a trinomial by expanding (you can use Symbolab’s calculator to do this part):
(x – 5)² = (x – 5)(x – 5) = x² – 10x + 25.

The trinomial is on order of degree, so we don’t need to do any additional steps.

What’s the Point of Writing Trinomials in Standard Form?

Writing a trinomial in standard form makes it easier to see the overall degree of the expression. For example, the expression 7x³ + 2x + 8x⁶ is not written in standard form, so it’s easy to make the mistake of thinking it’s a third degree trinomial (it’s actually a 6th degree). Writing expressions this way makes it easier to see very large and very small numbers.

Another reason to place expressions in standard form: if your trinomial is a linear equation, standard form makes it easier to find intercepts.