Pooled variance (also called combined, composite, or overall variance) is a way to estimate common variance when you believe that different populations have the same variances.
The pooled sample variance formula is:
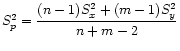
Where:
- n = the sample size for the first sample,
- m = the sample size for the second sample,
- S2x = sample variance for sample 1,
- S2y = sample variance for sample 2.
It’s unlikely you’ll actually need to use the formula though. Most statistical software has an option for pooled variance, like R or SPSS. You can also try this online calculator for Pooling the Means, and Variances.
The square root of pooled variance is the pooled standard deviation.
When Can I Use Pooled Variance?
If you believe the population variances are the same, one way to check that you might be able to use pooled variance is to calculate a ratio of sample standard deviations: ![]()
If this ratio is close to 1, then you can probably use pooled variance. This is a judgment call, but in general a ratio of 0.5 to 3 is a reasonable indication the variances are close enough (Penn State).
References
Penn State Eberly College of Science Department of Statistics. 7.3.1.1 – Pooled Variances. Retrieved February 25, 2020 from: https://online.stat.psu.edu/stat500/lesson/7/7.3/7.3.1/7.3.1.1