The midrank is a tied observation’s average rank. An observation’s rank is its position in an order list, from smallest to largest. A midrank is one way to deal with tied ranks in nonparametric tests that based on ranks, like the Wilcoxon rank-sum test. You can extend a test to allow for ties by “patching” the data and assigning midranks instead of ranks (Stark, 2021).
For example, let’s say your ordered observations were {1.3, 1.7, 1.7, 2.5}. These would be ranked {1, 2, 2, 4}. However, you take the average of where the two tied ranks should be (i.e. ranked 2 and 3} and report the ranks with midranks instead: {1, 2.5, 2.5, 4}.
Finding the Midrank
The midrank depends on the number of tied ranks (l) and number of items that are lower ranked (k). It can be found with the formula (Scholz, 2013):
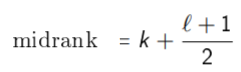
For example, the ordered observations given above {1.3, 1.7, 1.7, 2.5} have a mid-rank of 2.5:
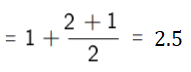
References
Agresti, A. (2003). Categorical Data Analysis. Wiley.
Scholz, F. (2013). Stat 425 Introduction to Nonparametric Statistics Rank Tests for Comparing Two Treatments. Retrieved February 14, 2021 from: http://faculty.washington.edu/fscholz/SpringStat425_2013/Stat425Ch1.pdf
Stark, P. (2021). SticiGui. Retrieved February 14, 2021 from: https://www.stat.berkeley.edu/~stark/Teach/S240/Notes/ch4.htm