How do you find function intervals?
You can find the intervals of a function in two ways: with a graph, or with derivatives.
Find function intervals using a graph
Example Question: Find the increasing intervals for the function g(x) = (⅓)x3 + 2.5x2 – 14x + 25
Step 1: Graph the function (I used the graphing calculator at Desmos.com). This is an easy way to find function intervals. Even if you have to go a step further and “prove” where the intervals are using derivatives, it gives you a way to check your answer.
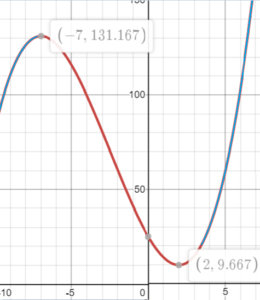
The function appears to be increasing in two intervals: (-∞, -7) and (2, ∞).
The problem with just graphing a function is you don’t know what’s happening off the graph. For example, you could zoom out a thousand times and never be quite sure that the graph isn’t going to do something strange, like a sudden drop. To be 100% sure of your answer, check it with the next few steps.
Find intervals using derivatives
You can think of a derivative as the slope of a function. If the slope (or derivative) is positive, the function is increasing at that point. If it’s negative, the function is decreasing. So to find intervals of a function that are either decreasing or increasing, take the derivative and plug in a few values.
Example Question: Find the increasing function intervals for g(x) = (⅓)x3 + 2.5x2 – 14x.
Step 1: Find the first derivative. For this particular function, use the power rule:
g′(x) = 3*(⅓)x3-1 + 2* 2.5x2-1 – 14x(1-1) + 99(0)
= x2 + 5x – 14
Step 2: Set the derivative equal to zero and solve (factoring often works):
x2 + 5x – 14 = 0
Factoring, we get:
(x – 2)(x + 7) = 0
Solving for x gives:
x = -7, x = 2.
Step 3: Create intervals on the number line with the x-values from Step 3.
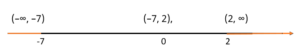
For this example, we have 3 intervals: (–∞, –7), (–7, 2), (2, ∞).
Step 4: Pick one point in each interval to “test”. You can choose any number in the interval, but you may want to pick a number like 0, 1, or 10 to make your calculations easier. For example, in the interval (–∞, –7), -10 is a good choice. For (–7, 2), let’s go with 0 and for (2, ∞), 10.
Step 5: Plug the values you chose in Step 5 into the derivative formula (from Step 1) to determine if the derivative has a positive or negative value. Our derivative formula is x2 + 5x – 14, so that gives:
- = -102 + 5(-10) – 14 = 36
- = 02 + 5(0) – 14 = -14
- = 102 + 5(10) – 14 = 136
The first derivative tells us that a function is increasing when the values for the first derivative are positive. Therefore, we can conclude that the increasing function intervals are (-∞, -7) and (2, ∞).