Effect Size > Pooled Standard Deviation
What is a Pooled Standard Deviation?
The Pooled Standard Deviation is a weighted average of standard deviations for two or more groups. The individual standard deviations are averaged, with more “weight” given to larger sample sizes.
Watch the video for an overview and calculation example:
Once the pooled standard deviation has been calculated, SDpooled is used in place of SD1 and SD2 in the formula for standard error. Along with an updated degrees of freedom formula (df = n1 + n2 – 2), the idea is that you would be able to get a better model for the sampling distribution of the sample mean.
Pooled standard deviations are used in many areas in statistics, including: effect size calculations, t-tests, and ANOVAs. They are also used in lab-based sciences like biology and chemistry, where they can be an indication for repeatability of an experiment.
How to Calculate the Pooled Standard Deviation
Cohen (1988) offers a couple of options for calculating the pooled standard deviation. The simplest is:
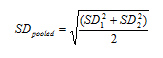
Where:
- SD1 = standard deviation for group 1
- SD2 = standard deviation for group 2
I’m including Cohen’s alternative formula here for reference, although there’s no clear benefit to using this one rather than the simpler formula above:
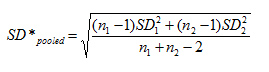
Where:
- x̄ = the sample mean
- n1 = sample size for group 1
- n2 = sample size for group 2
For three or more groups, change the “2” in the denominator to reflect the number of samples, k:
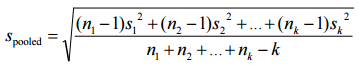
For equal sample sizes, the formula can be simplified to:
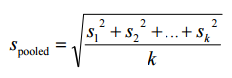
You can only use the above formulas if the standard deviations for the two groups are the same (this is because it would otherwise be violating the assumption of homogeneity of variances. If the standard deviations are different, run Hedge’s g or Glass’s Delta instead.
References
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education