Correlation Coefficients > Polychoric Correlation
What is Polychoric Correlation?
Polychoric correlation measures agreement between multiple raters for ordinal variables (sometimes called “ordered-category” data). Ordinal variables can be placed in order, but can’t be divided or multiplied. For example: a person’s level of depression, their level of disagreement or agreement, or how much they value possessions.
Calculating Polychoric Correlation
The polcyhoric coefficient was renowned in history for being difficult to calculate and involved calculus. The term “polychoric correlation” actually refers to a pre-computing table method using the polychoric series. The tables, developed by Karl Pearson, made the process a little easier but it’s now unusual to perform the calculation by hand; Software is almost always used and the calculations are made using the maximum likelihood method, not tables. Most statistical software has an option to find the coefficient. The input is usually a n*m contingency table.
- In SAS, use the CORR procedure (found here).
- SPSS doesn’t have a built in procedure, but it does have an extension command (SPSS HETCOR) which you can download from the SPSS community. (Click “Downloads for IBM SPSS Statistics”, then “Extension Commands” listed under “Extensions, Tools and Utilities”. Type HETCOR into the search box (top left) and then click on SPSSINC_HETCOR in the results list.
If you want to calculate the coefficient by hand, Mangal (2010) offers the following formula as a good approximation to the tetrachoric correlation:
cos(180/(√AD/BC)+1)
Where (AD/BC) is the odds ratio.
Interpreting the Results
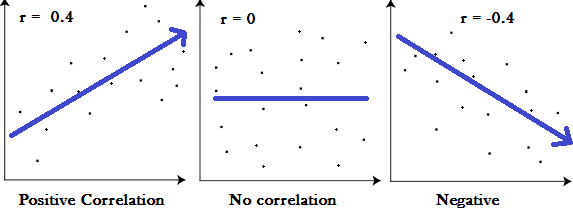
The polychloric is similar to linear correlation; The coefficient is between 0 and 1, where 0 is no relationship and 0 is a perfect relationship.
Reference:
Mangal, S.K. Statistics in Psychology and Education. Second edition. 2010.
Pearson, K. (1900). Mathematical contributions to the theory of evolution. VII. On the correlation of characters not quantitatively measurable. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci., 195 , 1–47. Available here.