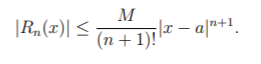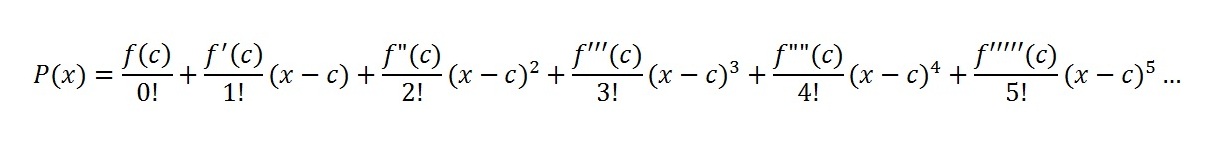
Many transcendental functions (e.g. logarithmic functions or trigonometric functions) can be expressed as these approximations; When you plug in cos 35° to a calculator, it doesn’t use a table to find that value: it uses a polynomial approximation.
Example of nth degree Taylor Polynomial
The function f(x) = e-x can be represented by an nth degree Taylor polynomial. The higher the “n”(degree), the better the approximation.
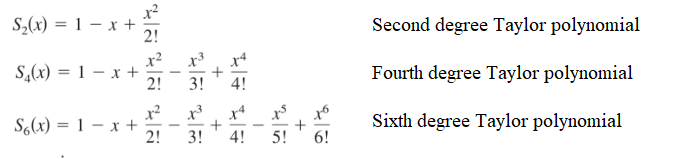
If it were possible to write an infinite number of degrees, you would have an exact match to your function. However, the goal here (like in many areas of calculus) isn’t to be “exact”, but to have an approximation that’s “good enough.” As you can’t write out an infinite number of sums, you choose a workable part (perhaps 10 or 20): this small part is called a partial sum.
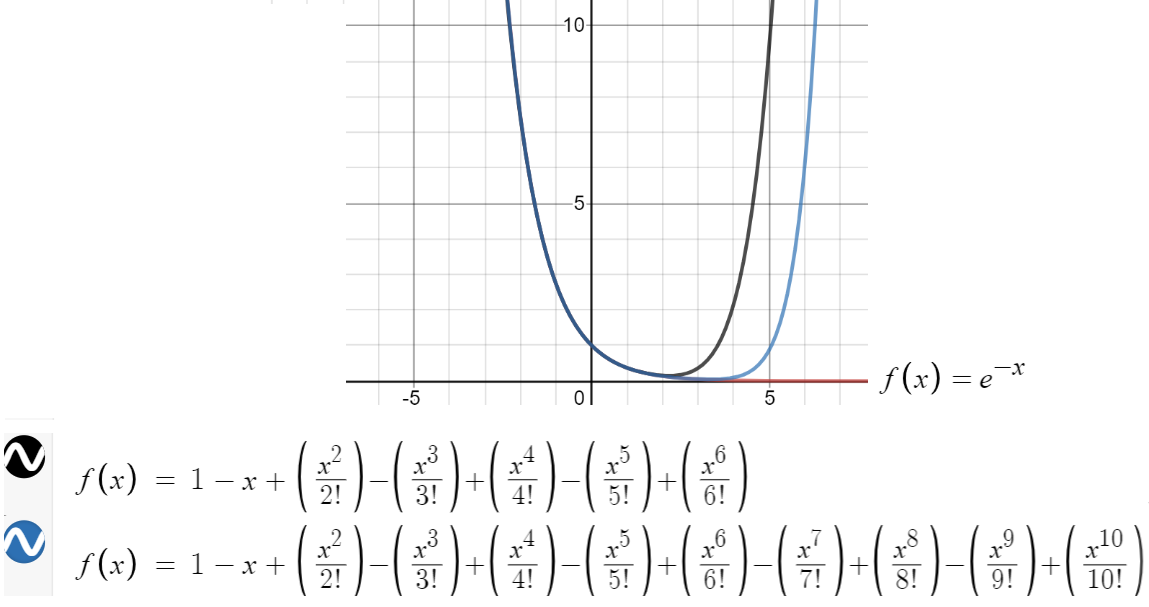
The following graph shows a tenth degree polynomial does a fairly good job at approximating the function (better than the sixth degree polynomial). Depending on what part of the function you’re working with, this may be good enough.
How Many Degrees is Good Enough?
Even the tenth degree (in blue) doesn’t do well at approximating the tail on the right of the above graph, so if you’re evaluating a function there you will want to go even higher with the number of degrees. How high should you go? How many terms is good enough? That can be answered with Taylor’s inequality, which states that (Lahodny, n.d.):
If |f(n + 1)(x) | ≤ M for |x – a| < R, then the remainder Rn(x) of the Taylor series satisfies
What’s the Difference Between a Taylor Polynomial and a Taylor Series?
A Taylor Series is the entire infinite sum of additions and multiplications, which can be represented in summation notation by
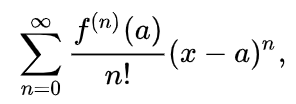
When you take a part of this series and create a smaller number of partial sums (like the ones I used above to graph approximations for e-x, those sums are called nth degree Taylor polynomials (or just “Taylor Polynomials” for short).
References
Lahodny, G. (2019). Section 10.9: Applications of Taylor Polynomials. Retrieved July 21, 2020 from: https://www.math.tamu.edu/~glahodny/Math152/Section%2010.9.pdf
Schwartz, S. (2017). AP® Calculus AB & BC All Access Book. Research & Education Association.
Graph: Demos.com