Notation for Differentiation: Types
There are a few different ways to write a derivative. The two most popular types are Prime notation (also called Lagrange notation) and Leibniz notation. Less common notation for differentiation include Euler’s and Newton’s.
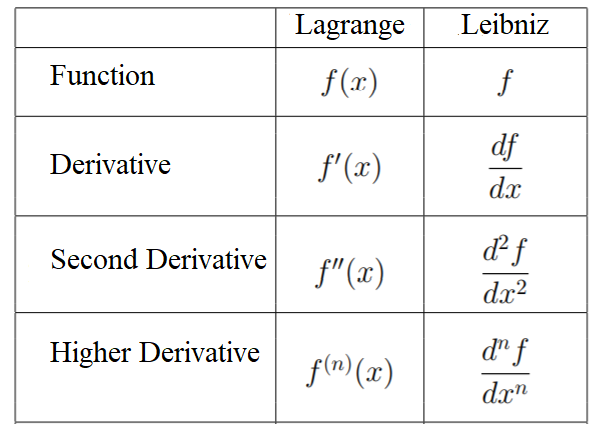
Derivative Notation #1: Prime (Lagrange) Notation
Prime notation was developed by Lagrange (1736-1813). You simply add a prime (′) for each derivative:
- f′(x) = first derivative,
- f′′(x) = second derivative,
- f′′′(x) = third derivative.
A prime symbol looks similar to an apostrophe, but they aren’t the same thing. They will look slightly different depending on the font on your screen, but don’t make the mistake of typing an apostophe ( ‘ ) when what you really need is a prime ( ′ ). While this may seem a little pedantic, a small difference has a big meaning, much in the same way a zero (0) has a vastly different meaning from the letter O.
Derivative Notation #2: Leibniz Notation
An equally popular notation for differentiation was introduced by Gottfried Wilhelm Leibniz (1646-1716). This notation uses dx and dy to indicate infinitesimally small increments of x and y:
![]()
The notation is a bit of an oddball; While prime notation adds one more prime symbol as you go up the derivative chain, the format of each Leibniz iteration (from “function” to “first derivative” and so on) changes in subtle yet important ways. The following table illustrates these changes and shows how they compare with the (simpler) prime notation:
Less Common Notation for Differentiation
This third type (developed by Newton in relation to the fluxion) has gone out of favor, but it’s worth a mention because it was once the most popular notation. You’ll come across it in some older texts:
![]()
Each dot represents a derivative, so two dots represent a second derivative, six dots represents the sixth derivative, and so on.
You’ll occasionally see a capital D (called Euler’s Notation after Leonhard Euler) to denote a derivative.
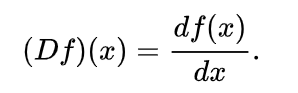
Higher derivatives are represented by the D raised to some power. For example, D5 is the fifth derivative.
You may also come across a curly d, used in partial differentiation:
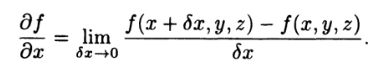
See also: Total Differential
References
Finan, Marcel B. Math 2243: Business Calculus. 2.3, Leibniz Notation of the Derivative. Retrieved from
https://faculty.atu.edu/mfinan/2243/business23.pdf on August 21, 2019.
McQuarrie, Barry. Barry McQuarrie’s Calculus II. Leibniz Notation for Derivatives. Retrieved from http://cda.mrs.umn.edu/~mcquarrb/teachingarchive/M1102/Resources/LeibnizNotation.pdf on August 21, 2019
Notation for Differentiation. Retrieved July 3, 2020 from: http://www.ma.man.ac.uk/~cds/articles/derivative.pdf