Hypothesis Testing > Neyman-Pearson Lemma
What is Neyman-Pearson Lemma?
The Neyman-Pearson Lemma is a way to find out if the hypothesis test you are using is the one with the greatest statistical power. The power of a hypothesis test is the probability that test correctly rejects the null hypothesis when the alternate hypothesis is true. The goal would be to maximize this power, so that the null hypothesis is rejected as much as possible when the alternate is true. The lemma basically tells us that good hypothesis tests are likelihood ratio tests.
The lemma is named after Jerzy Neyman and Egon Sharpe Pearson, who described it in 1933. It is considered by many to the theoretical foundation of hypothesis testing theory, from which all hypothesis tests are built.
Note: Lemma sounds like it should be a Greek letter, but it isn’t. In mathematics, a lemma is defined as an intermediate proposition used as a “stepping stone” to some other theorem. To differentiate the lemma from theories that have a name and a Greek letter (like Glass’s Delta or Fleiss’ kappa), it’s sometimes written as Lemma (Neyman-Pearson).
The “Simple” Hypothesis Test
The Neyman-Pearson lemma is based on a simple hypothesis test. A “simple” hypothesis test is one where the unknown parameters are specified as single values. For example:
- H0: μ = 0 is simple because the population mean is specified as 0 for the null hypothesis.
- H0: μ = 0; HA: μ = 1 is also simple because the population mean for the null hypothesis and alternate hypothesis are specified, single values. Basically, you’re assuming that the parameters for this test can only be 0, or 1 (which is theoretically possible if the test was binomial).
In contrast, the hypothesis σ2 > 7 isn’t simple; it’s a composite hypothesis test that doesn’t state a specific value for σ2.
Simple hypothesis tests — even optimized ones — have limited practical value. However, they are important hypothetical tools; The simple hypothesis test is the one that all others are built on.
The “Best” Rejection Region
Like all hypothesis tests, the simple hypothesis test requires a rejection region — the smallest sample space which defines when the null hypothesis should be rejected. This rejection region (defined by the alpha level) could take on many values. The Neyman-Pearson Lemma basically tells us when we have picked the best possible rejection region.
The “Best” rejection region is one that minimizes the probability of making a Type I or a Type II error:
- A type I error (α) is where you reject the null hypothesis when it is actually true.
- A type II error (β) is where you fail to reject the null hypothesis when it is false.
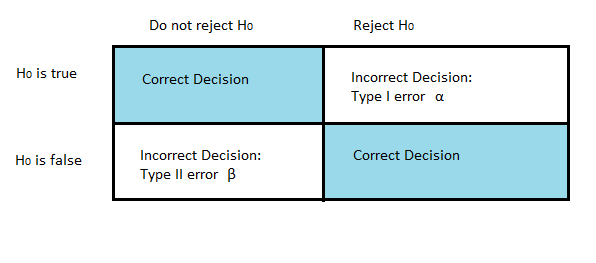
The probability that X is in the rejection region R is the statistical power of the test. The ideal scenario would be for both probabilities to be zero or at least extremely small. In the real world this isn’t possible, because a reduction in alpha often leads to an increase in beta and vice-versa. But we can get close — and that is what the lemma helps us with.
The Neyman-Pearson Lemma Defined
In order to understand the lemma, it’s necessary to define some basic principles about alpha/beta levels and power:
Alpha and Beta Levels
A Type I error under the null hypothesis is defined as:
Pθ(X ∈ R ∣ H0 is true),
Where:
- R = the rejection region and
- ∈ is the set membership.
A Type II error under the null hypothesis is defined as:
Pθ(X ∈ Rc∣ H0 is false),
Where:
- Rc = the complement of R.
Usually, an alpha level is set (e.g. 0.05) to restrict the probability of making a Type I error (α) to a certain percentage (in this case, 5%). Next, a test is chosen which minimizes Type II errors (β).
Power
Tests with a certain alpha level α can be written as:
Size α tests: sup β (θ) = α (θ ∈ Θ0)
Where:
- Θ0 = set of all possible values for θ under the null hypothesis
A level α test is one that has the largest power function. Mathematically, it is written as:
Level α test: sup β (θ) ≤α(Θ ∈ Θ0)
Definitions using UMP and Likelihood-Ratio
Casella and Berger (2002) use the above definitions to define a simple hypothesis test that is uniformly most powerful (UMP), which is the essence of the Neyman-Pearson Lemma:
“Let C be a class of tests for testing H0: θ ∈ Θ0 versus H1: θ ∈ Θc1. A test in class C, with power function β(θ), is a uniformly most powerful (UMP) class C test if β(θ) ≥ β′(θ) for every θ ∈ Θ0c and every β′(θ) that is a power function of a test in class C.
In plain English, this is basically saying:
The same statement can also be presented in terms of the likelihood ratio tests. Let’s say you had two simple hypotheses H0: θ = θ0 and H1:θ= θ1. In order to find the most powerful test at a certain alpha level (with threshold η), you would look for the likelihood-ratio test which rejects the null hypothesis in favor of the alternate hypothesis when
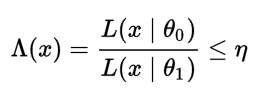
where
![]()
.
Variants
Dozens of different forms of the Neyman-Pearson Lemma (NPL) exist, each with different notations and proofs. They include variants by:
- Roussas (1997): Fundamental NPL for continuous random variables
- Casella and Berger (2002): NPL for continuous and discrete random variables
- Bain & Engelhardt (1990): Simplified NPL
- Lehmann (1991): a multidimensional variant of the NPL.
References:
Bain, Lee J., and Max Engelhardt. Introduction to Probability and Mathematical Statistics. 2nd ed. Boston: PWS-KENT Pub., 1992. Print
Casella, George, and Roger L. Berger. Statistical Inference. 2nd ed. Australia: Duxbury, 2002. Print.
Hallin, M. Neyman-Pearson Lemma. Wiley StatsRef: Statistics Reference Online. 2014.
Lehmann, E. L. Testing Statistical Hypotheses. Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced & Software, 1991. Print.
Roussas, George G. A Course in Mathematical Statistics. 2nd ed. San Diego, CA: Academic, 1997. Print.