The min-max theorem is a technique for finding the maximum and minimum values of a function. The theorems play a key role in computational complexity, game theory, and optimization.
Min-Max Theorem for Continuous Functions
The theorem states that if you have a closed interval I on a continuous function, then f will achieve it’s maximum value and minimum value on I. In formal terms, the theorem is as follows (Bényi, n.d.):
Let I = [a, b] ⊂ ℝ be a compact interval and f: I → ℝ a continuous function. Then f attains its maximum and minimum on I, that is, there exist u, v ∈ I such that
Where:
- ⊂ = subset of,
- ℝ = real numbers.
Despite a lot of notation, the theorem is pretty straightforward; A closed interval contains endpoints; While that doesn’t always mean that your minimum and maximums will happen at the endpoints (it could happen at the top of a curve in the middle of a graph, for example), it means that if they do happen there, then you know what those values are.
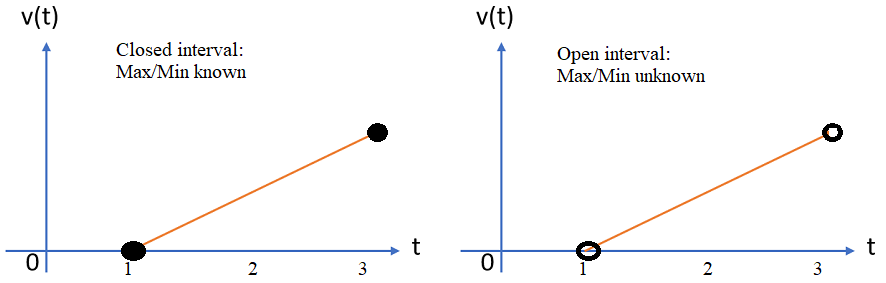
The above image shows the same function. On the left, you can see that the minimum value is 1 and the maximum value is 3. You can’t make that same call for the function on the right, as you don’t know the value at the endpoints. For example, the maximum value could be 2.99, or it could be 2.999999. While that seems like a pedantic distinction, that small amount between 2.99 and 2.99999 could results in large differences in any field where “small” changes lead to big results.
As this particular part of the theorem (for closed intervals) is relatively straightforward, proofs are usually not required. You can be positive that the absolute minimum and absolute maximum exist. But outside of that restrictive domain (i.e. the set of all functions with closed intervals), you can’t always be sure that the min and max exist.
Non Continuous Function Example
Let’s take a look at a noncontinuous function and it’s graph:
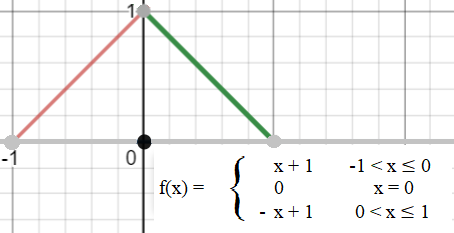
Although it looks like there’s a max somewhere around 0, we can’t be sure what that number is. The same is true for the minimum. We can use derivatives to find values at these points.
Next: Find absolute maximum using derivatives.
References
Bényi, Á. -4.6.6. The Minimum-Maximum Theorem, Retrieved July 23, 2020 from: http://faculty.wwu.edu/benyia/math312/min-max.pdf
Pardalos, P. (2013). Minimax and Applications. Springer US.