An n-tuple (also called an ordered n-tuple or just a list) is an ordered sequence of natural numbers (whole, non-negative numbers that we use to count), where n ≧ 1.
N-tuples are often denoted by an expression like (a1, a2, … a1). For example:
- 1-tuple (monad or singleton): (7)
- 2-tuple (pair or twin): (3, 4)
- 3-tuple (triple or triad): (3, 3, 7)
- 4-tuple (quadruplet): (3, 6, 7, 8)
- 5-tuple (quintuplet): (1, 3, 6, 7, 8)
- 6-tuple: (sextuplet):(4, 5, 7, 9, 11, 13)
A zero n-tuple (or empty function) has all-zero entries:
0 = (0, 0,…0).
Entries for tuples don’t have to be distinct (they can all be the same).
Addition of n-Tuples
Addition of tuples is easy. You just add the first components, then the second, and so on. For example, let’s say you bought 2 bags of rice and 3 cans of beans (2, 3), then went to a second store and bought 1 more bag of rice and 2 cans of beans (1, 2). The addition would be:
(2, 3)+
(1, 2)
= 3, 5
For this to work, your tuples must be the same size.
N-Tuples in Linear Algebra
If you’ve ever taken linear algebra, this type of addition (called component addition) might look familiar, with good reason: In matrices, an n-tuple is synonymous with “l x n matrix” (Rosen, 2013).
Tuples can be row matrices, like [0, 2, 3] or column matrices, such as
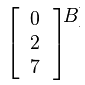
An n-tuple is commonly used to represent a vector. For example, the 2-tuple [3, 4] could represent a vector in 2D space where the tail of the vector is at the origin and head is at [3, 4]. Similarly, a 3-tuple like [-1, 4, 5] could represent a vector in 3D Space.
References
Cowin, S. & Doty, S. (2007). Tissue Mechanics. Springer, New York.
Davis, M. (2013). Computability and Unsolvability. Dover Publications.
Dr. Math. (1999). Definition of an N-tuple – Math Forum – Ask Dr. Math. Retrieved July 24, 2020 from: http://mathforum.org/library/drmath/view/55500.html
Rosen, G. (2013). Formulations of Classical and Quantum Dynamical Theory. Academic Press.