The Mercator series (also called the Newton-Mercator series or Dirichlet eta function of 1) is the series expansion for ln (1 + x).
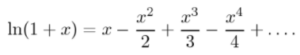
The series can be derived from the Taylor series, but it can be “tricky” to make the remainder vanish. Alternatively, it can also be derived from the finite geometric series (Jeffery, 2008).
The alternating harmonic series
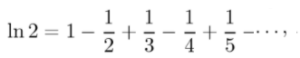
is the x = 1 case of the Mercator series. For larger values of x, the series does not converge at all (Hairer & Wanner, 2008).
History of the Mercator Series
The series is named after the Danish mathematician Nicolas Mercator (1620-1687) who first published the series in his book Logarithmotechnia. However, Newton was the first to find it although he did so independently (Hairer & Wanner, 2008).
Historically, the series was used to calculate logarithms. However, when Mercator first wrote about the series, the logarithm with base e hadn’t yet been introduced (Cajori, 1913); Therefore, Mercator didn’t actually write in terms of log(1 + x)—although he was the first to use the term “natural logarithm”. It was much later that the series was related to log (1 + x) and called the Mercator series.
Using Mercator’s Series
Mercator’s series has limited practical uses, as many other, faster, methods exist to calculate logarithms and find series. However, it is interesting from a purely mathematical standpoint.
Example Question:Use Mercator’s series to find a series for ln(2).
Solution. First, note that the definition of the series is ln (1 + x). So to find the series for ln(2), we need to rewrite ln (2) as ln (1 + 1). You now have the x-value (1) to place in the series expansion:
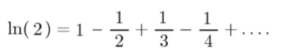
References
Cajori, F. (1913). History of the exponential and logarithmic concepts, American Math Monthly, vol.20(1913)1, p.12.
Hairer, E. & Wanner, G. (2008). Analysis by Its History. Springer.
Jeffery, D. (2008). Mathematical Physics Problems. Retrieved October 21, 2020 from: http://www.physics.unlv.edu/~jeffery/course/c_math/homewk/exambank.pdf