The Marascuilo procedure is used when you obtain a significant result (i.e., you reject the null hypothesis) for the chi-squared test for c proportions [1]. In other words, you would use the procedure if the chi-squared test indicated the population proportions are not the same across all groups. The Marascuilo procedure is only used for multiple (three or more) proportions.
The chi-squared test looks for significant differences between observed and expected data distributions among categories. If you get a significant result, one or more of the proportions are not the same, but the chi-square test won’t tell you which proportions are different. The Marascuilo procedure will compare all pairs and determine which proportions are statistically significant.
The following table shows an example of Multiple comparisons of incidences using the Marascuilo procedure [2]:

Equations for the Marascuilo procedure
The procedure works by finding the absolute differences between pairs of proportions. The absolute values of the differences are the test statistics.
Next, compute the test statistic using the equation
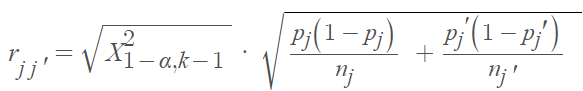
Where:
- Χ2U = Chi-square upper,
- p = sample proportions,
- n = sample size.
The Marascuilo procedure compares the sample differences with critical range differences. A pair is significantly different fs the absolute difference is larger than the critical range:
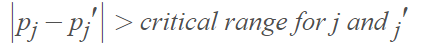
The pairs that have a test statistic larger than the critical value are significantly different [3].
References
[1] Basic Business Statistics. Chapter 12 Student Lecture Notes 12-1. Retrieved March 30, 2022 from: http://www3.govst.edu/kriordan/files/gsu610files/ppt/PDF/chap12.pdf
[2] Adeidia et. al. (2020). Assessment of Hypertension-Induced Deaths in Ghana: A Nation-Wide Study from 2012 to 2016. Journal of Data Analysis and Information Processing, 2020, 8, 158-170.
[3] Wagh, S. & Razvi, N. Marascuilo Method of Multiple Comparisons (An Analytical Study of Caesarean Section Delivery). Retrieved March 20, 2022 from: http://www.ijcmr.com/uploads/7/7/4/6/77464738/_marascuilo_method_of_multiple_comparisons__an_analytical_study_of_caesarean_section_delivery___.pdf