The M-estimator is a robust regression method often used as an alternative to the least squares method when data has outliers, extreme observations, or does not follow a normal distribution.
While the “M” indicates that M estimation is of the maximum likelihood type (Susanti et. al, 2013), M-estimators are actually a broad class of estimators that include the maximal likelihood estimator (Jureckova & Picek, 2005). Least squares estimators and LAV Estimators are also both special cases of M-estimation (Anderson, 2008).
When to Use the M-Estimator
The M-estimator is more efficient than Ordinary Least Squares (OLS) under certain conditions:
- Your data contains y outliers,
- The model matrix X is measured with no errors (Anderson, 2008).
M-estimators are especially useful when your data has outliers or is contaminated because one outlier (or heavy tailed errors) can render the normal-distribution based OLS useless; In that case, you have two options: remove the badly-behaving outliers, or use the robust M-estimator.
M-estimation isn’t recommended when:
- Anomalous data reflects the true population, or
- The population is made up of distinct mixture of distributions (Little, 2013).
How M Estimation Works
M estimation attempts to reduce the influence of outliers by replacing the squared residuals in OLS by another function of the residuals:
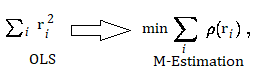
References
Anderson, R. (2008). Modern Methods for Robust Regression, Issue 152. SAGE. Retrieved October 14, 2019 from: https://books.google.com/books?id=ce5yKCu8HRoC
Fox, J. & Weisburg, S. (2013). Robust Regression.
Little, T. The Oxford Handbook of Quantitative Methods in Psychology. Retrieved October 14, 2019 from: https://books.google.com/books?id=kOqOqVMgfzYC
Jureckova, J. & Picek, J. (2005). Robust Statistical Methods with R. CRC Press.
Susanti, Y. et al. (2013). M Estimation, S. Estimation, and MM Estimation in Robust Regression. Retrieved October 14, 2019 from: https://ijpam.eu/contents/2014-91-3/7/7.pdf