The definition of an infinite product is very similar to the definition of an infinite sum. Instead of adding an infinite number of terms, you’re multiplying. For example, 1·2·3·,…,∞.
More formally, let {xn} represent a numerical series. The infinite product of the numbers x
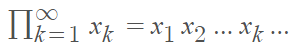
And the nth partial product is:
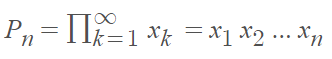
At first glance, the two formulas may seem identical. However, note the terminating xn in the second formula, indicating the end of the partial sum.
We can define convergence for infinite products in a couple of different ways. The product is convergence if either
Infinite sums and products are widely used in applied mathematics and analysis as well as number theory.
Infinite Product Examples
One of the earliest infinite products is the Wallis formula, gives an expansion for π as an infinite product:
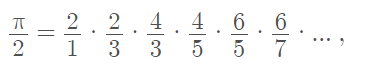
Which can be written, equivalently, in product notation:
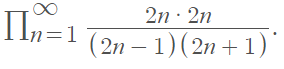
The Euler formula is another famous infinite product. It is defined as [3]:
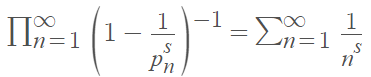
Where:
- pn is the nth prime,
- The right hand side is the Riemann zeta function.
Infinite Product Formula Example
Expressing a function as an infinite product makes it easier to see where the zeros of a function are. As a simple example, the polynomial function f(x) = x – x3 can be factored as a product:
f(x) = x – x3 = x(1 – x2) = x(1 – x)(1 + x)
This makes it clearer that the zeros are at x = 0, x = 1, or x = -1.
In the same way, sin(πx) can be rewritten as an infinite product formula [4]:
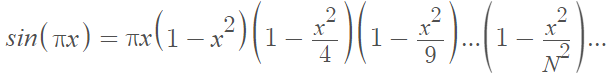
References
[1] Mahmudov, E. (2013). Single Variable Differential and Integral Calculus. Atlantis Press.
[2] Kuratowski,, K. & Lohwater, A. (2014). Introduction to Calculus, Elsevier Science p.74.
[3] 2.6. Infinite Products. Retrieved August 17, 2021 from: https://www.math.uh.edu/~shanyuji/Complex/complex-1/cx-11-online.pdf
[4] Smith, M. Math 1320 Lab EC. Retrieved August 17, 2021 from: http://www.math.utah.edu/~msmith/pastteaching/1320/labEC.pdf