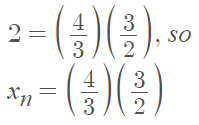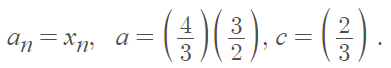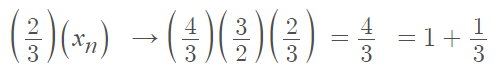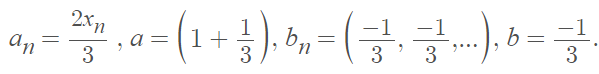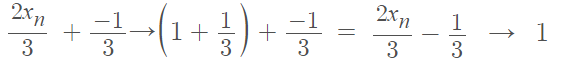Contents:
In a nutshell, the algebraic limit theorem and order limit theorem are very similar in that they both describe limits for bounded convergent sequences. While the algebraic theorem uses +, –, *, and ÷, the order theorem uses ≤ and ≥.
What is the Algebraic Limit Theorem?
The algebraic limit theorem shows us that sequences behave in an orderly fashion when subjected to mathematical operations.
Formally stated, the algebraic limit theorem is [1]:
If a = lim an and b = lim bn, then
- lim(can) = ca for all c ∈ ℝ,
- lim(an + bn) = a + b,
- lim(anbn) = ab,
- lim(an/bn) = a/b provided b ≠ 0.
Each of these statements has their own proof. For example, the proof for the first statement is as follows:
Proof [2]: Assuming that c ≠ 0, the goal is to show the sequence converges to c · a.
- Let ε = an arbitrary positive number. We want to find the point in the sequence where |can – ca| < ε.
- |can – ca| = |c| |an – a|
- Choose an N so that:
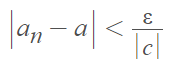
This is true whenever n ≥ N. Here, we’re making N very, very small. - Show that N works. For all n ≥ N:
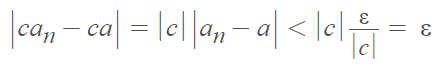
Algebraic Limit Theorem Example: A Worked Proof [3]
Example question: Show that If (xn) → 2, then ((2xn – 1)/3) → 1.
- Start with the given information: Xn → 2.
- Rewrite as a pair of fractions:

- Let:

- Substitute the values into the algebraic limit theorem, which tells us that can → ca. This results (with a little numerical manipulation) in:

- Let:

- We know by the Algebraic Limit Theorem that an + bn → a + b., so:

Alternative Definition for Functions
The algebraic limit theorem for functions is similar to the basic definition, except it is rewritten in function notation. For a limit x→p, the theorem is:
- lim (f(x) + g(x)) = lim f(x) + lim g(x)
- lim (f(x) – g(x)) = lim f(x) – lim g(x)
- lim (f(x) · g(x)) = lim f(x) · lim g(x)
- lim (f(x) / g(x)) = lim f(x) / lim g(x)
The indeterminate limits (on the left) may exist even when the limits on the right do not. If any of the theorems don’t give you a limit, try an alternate method like the sandwich theorem or L’Hospital’s rule.
What is the Order Limit Theorem?
Suppose a = lim an and b = lim bn. The order limit theorem states that [1]:
- If an ≥ 0 for all n ∈ ℕ, then a ≥ 0.
- If an ≤ bn for all n ∈ ℕ, then a ≤ b.
- Assuming there is a c ∈ ℝ:
- If c ≤ bn for all n ∈ ℕ, then c ≤ b.
- If an ≤ c for all n ∈ ℕ, then a ≤ c.
References
[1] Bakker, L. Math 341 Lecture #8. §2.3: The Algebraic and Order Limit Theorems. Retrieved August 19, 2021 from: https://math.byu.edu/~bakker/M341/Lectures/Lec08.pdf
[2] Chapter 2: Sequence and Series. Retrieved August 19, 2021 from: http://econdse.org/wp-content/uploads/2018/08/sequence-reading.pdf
[3] Lytle, B. Introduction to the convergence of sequences. Retrieved August 19, 2021 from: https://math.uchicago.edu/~may/REU2015/REUPapers/Lytle.pdf