Horizontal Line Test
The horizontal line test tells you if a function is one-to-one. It’s also a way to tell you if a function has an inverse.
Watch the video or read on below:
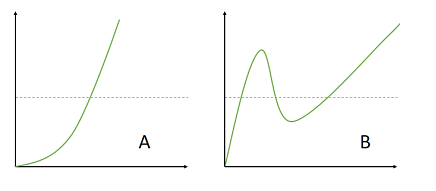
If any horizontal line can cross the graph at most once, then the function is one-to-one.
It works in a similar way to the vertical line test, except you (perhaps, obviously) draw horizontal lines instead of vertical ones. The two tests also give you different information.
- The vertical line test tells you if you have a function,
- The horizontal test tells you if that function is one to one.
Inverses
The horizontal line test lets you know if a certain function has an inverse function, and if that inverse is also a function. Only one-to-one functions have inverses, so if your line hits the graph multiple times then don’t bother to calculate an inverse—because you won’t find one.
The horizontal line test can get a little tricky for specific functions. For example, at first glance sin x should not have an inverse, because it doesn’t pass the horizontal line test. However, if you take a small section, the function does have an inverse. For example, on the interval [–π/2, π/2], y = sin x is one-to-one and therefore has an inverse for that interval.
Horizontal Line Test vs. Vertical
The vertical line test tells you if you have a function, while the horizontal line test tells you if that function is one to one (injective).
Always perform the horizontal line test after the vertical line test. That’s because it’s quite possible for an equation to pass the vertical line test, but not the horizontal line test. What this means is that you might end up thinking you have a one-to-one function (because it passed the horizontal test), but in actual fact you don’t have a function at all (because it failed the vertical one).
References
Young, C. (2010). Precalculus. John Wiley and Sons.