What is the Gregory–Newton Interpolation Formula?
The Gregory–Newton interpolation formula is defined as
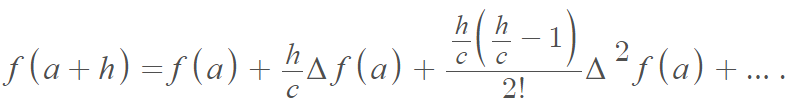
Where:
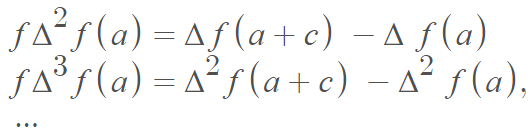
The Taylor series is the limiting case of the formula as c → 0 [1].
Using the Formula to Find Function Values
The formula is perhaps best known for its ability to calculate a function value at an arbitrary point from the value (a + h) at an arithmetic sequence of points a, a + b, a + 2b,….
To calculate a value for f(x), for any x between known values, replace h in the formula with x – a. This isn’t necessarily the true function value, but rather a value for a polynomial in h that equals the function values at a, a + c, a + 2c,… [2]. Therefore, the formula is valid for any function that is the limit of its own polynomial approximation (i.e., any functions that can be represented by a power series) [3].
Gregory–Newton Interpolation Formula for Integration
You can also use the same formula to approximate integrals [2]. Let’s say you had a function g(x) that you want to integrate:
- Use g(x) values to get g(a), g(a + c), g(a + 2c),…
- Find the differences of the values you obtained in Step 1, along with their higher-order differences.
- Substitute your solutions from Step 2 into the formula.
These steps will give you a polynomial approximation for your function, which can be integrated easily—giving you your approximate integral.
History
Both Newton and Gregory were inspired by Wallis’s loose heuristic method of interpolation [2]. Gregory discovered the general formula first, followed by an independent discovery by Newton. Both mathematicians used to formula to derive the binomial theorem. However, while Newton sketched a proof for the formula, Gregory did not [2].
References
[1] Vacher, H. Computational Geology 16: The Taylor Series and Error Propagation. Journal of Geoscience Education, v. 49, n.3, p. 305-313, May 2001 (edits, June 2005).
[2] Kline, M. (1990). Mathematical Thought from Ancient to Modern Times: Volume 2. OUP USA.
[3] Stillwell, J. Mathematics and Its History. 3rd Edition. Springer.