Many functions cannot be expressed as a power series a0 + a1x + a2x2 + …. For example, any functions that tend to infinity as x → 0 have value a0 when x →0, so are not expressible as power series. Functions with fractional powers of x, like x½, are also problematic, because of branching behavior at zero (i.e., they are multivalued at zero and so are not “true” functions at that point). In fact, most algebraic functions have some kind of multi-valued points and so cannot fit a traditional power series, where one value must be placed for every x in the series. The solution is a fractional power series, the discovery of which is credited to Isaac Newton. Puiseux (1850) applied more rigor to the topic; it is for this reason that fractional power-series expansions of algebraic functions are called Puiseux expansions [1], Puiseaux series [2], or sometimes, the Newton-Puiseaux method.
The method has many practical applications, especially in engineering. For example, it can be used in thermodynamics to solve systems of fractional differential equations [3].
Formula for the Fractional Power Series
The general formula for the fractional power series is
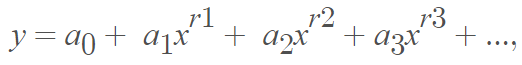
Where rk are rational numbers (rational numbers can be expressed as fractions).
The series can be rewritten as a finite sum of a traditional power series. The powers of x get rewritten as multipliers:
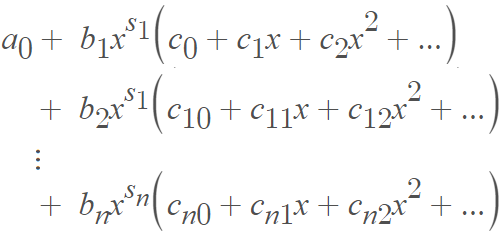
The result is that the behavior of y, in the neighborhood of x = 0, acts like a finite sum of fractional powers.
Example
If y2(1 + x)2, then:
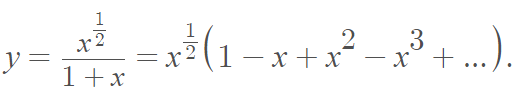
Near x = 0, y will behave similarly to x½.
References
[1] Puiseux Series and Algebraic Solutions of First Order Autonomous AODEs — A MAPLE Package.
[2] Stillwell, J. (2010). Mathematics and Its History. 3rd Edition. Springer.
[3] Ren, F. & Hu, Y. (2018). The fractional power series method an efficient candidate for solving fractional systems. Thermal Science 22(4):1745-1751.