Derivatives > Derivative of Tan x
What is the Derivative of Tan x?
The derivative of tan x is sec2x:
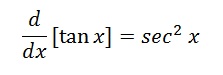
See also:
How to Take the Derivative of Tan x
You can take the derivative of tan x using the quotient rule. That’s because of a basic trig identity, which is a quotient of the sine function and cosine function:
Step 1: Name the numerator (top term) in the quotient g(x) and the denominator (bottom term) h(x). You could use any names you like, as it won’t make a difference to the algebra. However, g(x) and h(x) are common choices.
- g(x) = sin(x)
- h(x) = cos(x)
Step 2: Put g(x) and h(x) into the quotient rule formula.
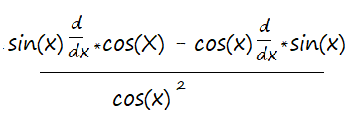
Note that I used d/dx here to denote a derivative (Leibniz Notation) instead of g(x)′ or h(x)′ (Prime Notation (Lagrange), Function & Numbers). You can use either notation: they mean the same thing.
Step 3: Differentiate the functions from Step 2. There are two parts to differentiate:
- The derivative of the first part of the function (sin(x)) is cos(x)
- The derivative of cos(x) is -sin(x).
Placing those derivatives into the formula from Step 3, we get:
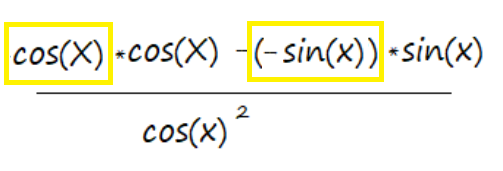
Which we can rewrite as:
f′(x) = cos2(x) + sin2(x) / cos(x)2.
Step 4: Use algebra / trig identities to simplify.
- Specifically, start by using the identity cos2(x) + sin2(x) = 1
- This gives you 1/cos2(x), which is equivalent in trigonometry to sec2(x).
Proof of the Derivative of Tan x
There are a couple of ways to prove the derivative tan x. You could start with the definition of a derivative and prove the rule using trigonometric identities. But there’s actually a much easier way, and is basically the steps you took above to solve for the derivative. As it relies only on trig identities and a little algebra, it is valid as a proof. Plus, it skips the need for using the definition of a derivative at all.
Steps
Example problem: Prove the derivative tan x is sec2x.
Step 1: Write out the derivative tan x as being equal to the derivative of the trigonometric identity sin x / cos x:
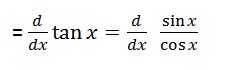
Step 2: Use the quotient rule to get:
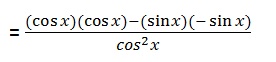
Step 3: Use algebra to simplify:
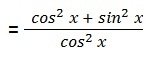
Step 4: Substitute the trigonometric identity sin
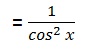
Step 5: Substitute the trigonometric identity 1/cos2x = sec2x to get the final answer:
d/dx tan x = sec2x
That’s it!
References
Nicolaides, A. (2007). Pure mathematics: Differential calculus and applications, Volume 4. Pass Publications.