A one sided derivative is either a derivative from the left or a derivative from the right.
- Derivative from the left: You approach a point from the left direction of the number line.
- Derivative from the right: You approach a point from the right direction of the number line.
These are particularly useful at endpoints, where a function stops abruptly and doesn’t go beyond a certain point.

Any function that is differentiable at the end of its domain is called one sided differentiable (Reinholz, n.d.).
Note though, that if both the right and left hand derivatives are equal, the derivative is an ordinary derivative, not a one sided derivative. Ordinary derivatives are the ones you’re normally used to dealing with in calculus; Another way to define them is that they are not partial derivatives.
A More Formal Definition of a One Sided Derivative
A one sided derivative can be defined more formally as (Fogel, n.d.):
If f is a function on a half closed interval [a, b), then:
The right hand derivative at a, denoted f′– is the number
![]()
If it exists,
And
If the function is also defined on a half closed interval
(a, b], then:
The left hand derivative at b, denoted f′+ is the number
![]()
If it exists.
Connection with Limits
In a practical sense, one sided derivatives are analogous to one sided limits.
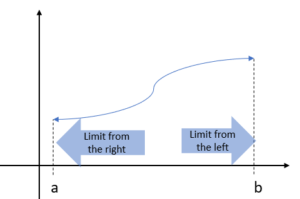
See also: One sided limits.
References
Aramanovich, I. et al. (2014). http://Mathematical Analysis: Differentiation and Integration [Print Replica]. Pergamon.
Fogel, M. The Derivative. Retrieved December 29, 2019 from: http://staff.imsa.edu/~fogel/Analysis/PDF/25%20The%20Derivative
Hazelwinkle, M. (1990). Encyclopedia of Mathematics. Springer.
Math Boys. Absolute Value Function. Retrieved August 2019 from: https://www.statisticshowto.com/absolute-value-function/
Reinholz, D. Derivatives. Retrieved December 29, 2019 from: https://www.ocf.berkeley.edu/~reinholz/ed/08sp_m160/lectures/derivatives.pdf