Communality: Definition, Examples

In PCA and Factor Analysis, a variable’s communality is a useful measure for predicting the variable’s value. More specifically, it tells you what proportion of the variable’s variance is a result of either:

The principal components or
The correlations between each variable and individual factors (Vogt, 1999).

In Factor Analysis, communality may be denoted as h².

Values for Communality

A variable’s communality ranges from 0 to 1.

In general, one way to think of communality is as the proportion of common variance found in a particular variable.

A variable that doesn’t have any unique variance at all (i.e. one with explained variance that is 100% a result of other variables) has a communality of 1.
A variable with variance that is completely unexplained by any other variables has a communality of zero (Field, 2013).

Relation to Error and Specific Variance

Communality (aka common variance) is intertwined with unique variance. The two types of variance make up 100% of the variable’s variance.

Unique variance is in turn made up of specific variance and error variance. Specific variance has something specific to do with your model/survey. For example, if you were performing factor analysis on results from a questionnaire to evaluate depression, a recent divorce would certainly account for some variance. Something fairly unrelated (like the subject didn’t get any sleep the night before the test because they were binge watching Friends) would be error variance.

The relationship between all of these different types of variance is best explained with an image:

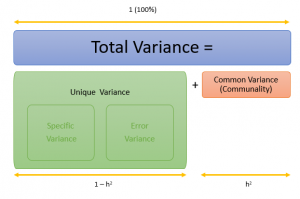
Communality in PCA

One way to define communality is in terms of the sum of squared loadings on each principal component (McGarigal et al., 2013):

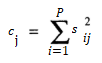
Where:

c_j = communality of the jth variable
s_ij = loading (or correlation) between the ith component and the jth variable.

References

Field, A. (2013). Discovering Statistics Using IBM SPSS Statistics. SAGE.
McGarigal et al. (2013). Multivariate Statistics for Wildlife and Ecology Research. Springer Science & Business Media.
Sapp, M. (2006). Basic Psychological Measurement, Research Designs, and Statistics Without Math. Charles C Thomas Publisher.
Vogt, W. P. (1999). Dictionary of Statistics and Methodology A Non-Technical Guide for the Social Sciences (2nd ed.). London Sage Publications