A combined mean is a mean of two or more separate groups, and is found by :
- Calculating the mean of each group,
- Combining the results.
Combined Mean Formula
Watch the video for two worked examples using the combined mean formula:
A combined mean for two sets can be calculated by the formula
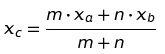 :
:
Where:
- xa = the mean of the first set,
- m = the number of items in the first set,
- xb = the mean of the second set,
- n = the number of items in the second set,
- xc the combined mean.
A combined mean is simply a weighted mean, where the weights are the size of each group.
For more than two groups:
- Add the means of each group—each weighted by the number of individuals or data points,
- Divide the sum from Step 1 by the sum total of all individuals (or data points).
Calculating a Combined Mean: Examples
Suppose you are running a survey on math proficiency (as measured by an achievement test) in kindergarten, and you have results from two different schools.
- In school 1, 57 kindergarteners were tested and their mean score was 82.
- In school 2, 23 kindergartners were tested and their mean score was 63.
The combined mean can be calculated by plugging in our numbers into the formula given above:
[(57*82)+(23*63)]/(57+23) = 76.5.
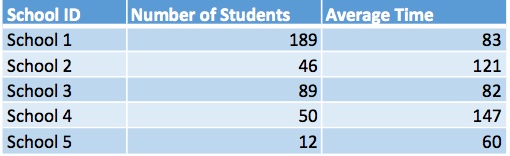
Now suppose you were running a survey on reading speed, as measured by how long it took 1st graders to read a given block of text. Your results come in for five schools:
To calculate the combined mean:
- Multiply column 2 and column 3 for each row,
- Add up the results from Step 1,
- Divide the sum from Step 2 by the sum of column 2.
((189*83) + (46*121) + (89*82) + (50*147) + (12*60)) / (189 + 46 + 89 + 50 + 12) = 94.87
Plug that in your calculator, and the answer you get—94.87—is the combined mean for all five schools; the average reading time for all students.
This same method may be used to combine any number of means.
References
Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Kotz, S.; et al., eds. (2006), Encyclopedia of Statistical Sciences, Wiley.
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.