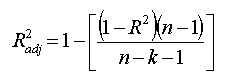Adjusted R2: Overview
Adjusted R2 is a special form of R2, the coefficient of determination.
Watch the video for an overview

R2 shows how well terms (data points) fit a curve or line. Adjusted R2 also indicates how well terms fit a curve or line, but adjusts for the number of terms in a model. If you add more and more useless variables to a model, adjusted r-squared will decrease. If you add more useful variables, adjusted r-squared will increase.
Adjusted R2 will always be less than or equal to R2.
You only need R2 when working with samples. In other words, R2 isn’t necessary when you have data from an entire population.
- N is the number of points in your data sample.
- K is the number of independent regressors, i.e. the number of variables in your model, excluding the constant.
If you already know R2 then it’s a fairly simple formula to work. However, if you do not already have R2 then you’ll probably not want to calculate this by hand! (If you must, see How to Calculate the Coefficient of Determination). There are many statistical packages that can calculated adjusted r squared for you. Adjusted r squared is given as part of Excel regression output. See: Excel regression analysis output explained.
Meaning of Adjusted R2
Both R2 and the adjusted R2 give you an idea of how many data points fall within the line of the regression equation. However, there is one main difference between R2 and the adjusted R2: R2 assumes that every single variable explains the variation in the dependent variable. The adjusted R2 tells you the percentage of variation explained by only the independent variables that actually affect the dependent variable.
How Adjusted R2 Penalizes You
The adjusted R2 will penalize you for adding independent variables (K in the equation) that do not fit the model. Why? In regression analysis, it can be tempting to add more variables to the data as you think of them. Some of those variables will be significant, but you can’t be sure that significance is just by chance. The adjusted R2 will compensate for this by that penalizing you for those extra variables.
While values are usually positive, they can be negative as well. This could happen if your R2 is zero; After the adjustment, the value can dip below zero. This usually indicates that your model is a poor fit for your data. Other problems with your model can also cause sub-zero values, such as not putting a constant term in your model.
Problems with R2 that are corrected with an adjusted R2
- R2 increases with every predictor added to a model. As R2 always increases and never decreases, it can appear to be a better fit with the more terms you add to the model. This can be completely misleading.
- Similarly, if your model has too many terms and too many high-order polynomials you can run into the problem of over-fitting the data. When you over-fit data, a misleadingly high R2 value can lead to misleading projections.
References
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.