Abel’s Inequality: Definition & Proof

Calculus Definitions >

Abel’s Inequality, named after 19th Century Norwegian mathematician Niels Abel, is an estimate for the sum of products of two numbers.

Let’s a_k and b_k are two sets of numbers. First, let’s look at the numbers b_k and say that the absolute value of all sums B_k = b₁ + … + b_k , k = 1, …, n are less than or equal to another number, B. Now consider a_k. If either of the following are true:

1. a_i ≥ a_{i + 1} or
2. a_i ≤ a_{i + 1, i = 1, 2, …, n – 1}

then [1]:


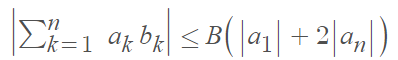
If the set of numbers a_k is non-increasing and non-negative, the inequality simplifies to:

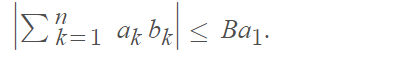
Uses for Abel’s inequality include:

• Giving a bound for the absolute value of the inner product of two vectors.
• Investigating convergence of sums,
• Showing that certain partial sums form a Cauchy sequence.

Alternative Definition’s of Abel’s Inequality

There are a few different ways to define the inequality.

One way to define it is as an inequality [2], stating that if g is monotone, then


is bounded above by:

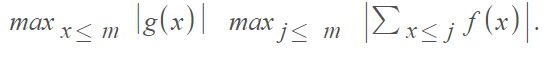
For example, if, for all values of n,
A > u₁ + u₂ + … + u_n > B,
Where u_i are real-valued quantities, and if a₁, a₂, …, a_n are a series of positive quantities that constantly decrease as n increases, then:
a₁A > a₁ u₁ + a₂ u₂ + … a_n u_n > a₁B.

It can also be stated as [3]
Let z₁, …, z_n ∈ ℂ, and let S_k = z₁ + … + z_k, for all k. Then, for each sequence of real numbers a₁ ≥ a₂ ≥ … ≥ a_n ≥ 0:

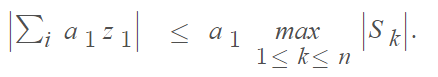
Proof of Abel’s Inequality

We have a_n = s_n − s_n − 1, so [4]:


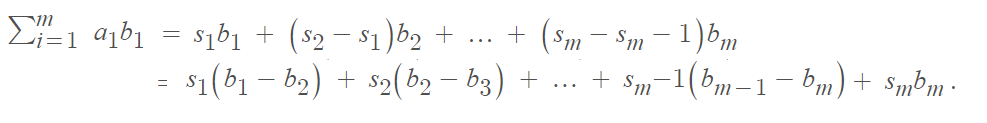
Every |s_n| ≤ M and b_n − b_{n + 1} is positive, so
|s_n(b_n − b_n+1)| ≤ M(b_n − b_{n + 1}).

By the triangle inequality*:



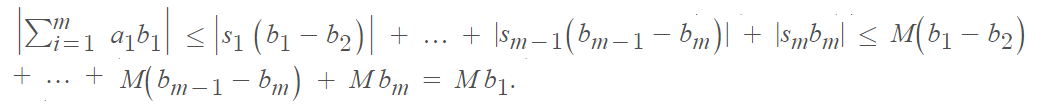
*The Triangle Inequality d(x, y) + d(y, z) ≥ g(x, z) states that the third side of a triangle is always less than the sum of its two sides (or equal, in the case that all points are on a straight line).

References

[1] Abel inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abel_inequality&oldid=34411
[2] Wolf, J. Sets Whose Difference Set is Square-Free. Retrieved July 3, 2021 from: https://www.cs.umd.edu/~gasarch/TOPICS/vdw/wolfsq.pdf
[3] Ferber, A. (2020). Arbitrary Topics. Retrieved July 3, 2021 from: https://cpb-us-e2.wpmucdn.com/faculty.sites.uci.edu/dist/f/842/files/2020/06/Inequalities.pdf
[4] Azoff, E. (2010). Sequences and Series. Retrieved July 3, 2021 from: http://alpha.math.uga.edu/~azoff/courses/3100sp10.pdf