A Cauchy sequence is a sequence of real numbers with terms that eventually cluster together—if the difference between terms eventually gets closer to zero. Whether or not a sequence is Cauchy is determined only by its behavior: if it converges, then it’s a Cauchy sequence (Goldmakher, 2013).
More formally, the definition of a Cauchy sequence can be stated as:
“A sequence (an) is called a Cauchy sequence if for every ε > 0, there exists an N ∈ ℕ such that whenever m, n ≥ N, it follows that |am − an| < ε” ~ (Amherst, 2010)
In plain English, this means that for any small distance (ε), there is a certain value (or set of values). Once the terms go past this value, any two terms are within that distance of each other.
For example, the following sequence is Cauchy because it converges to zero (Gallup, 2020):
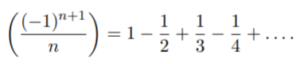
Graphically, a plot of a Cauchy sequence (defined in a complete metric space) tends towards a certain number (a limit):
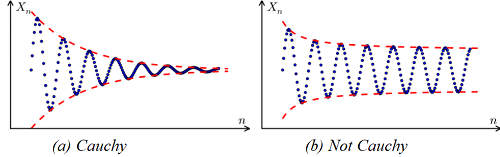
Properties of a Cauchy Sequence
- Every convergent sequence is a Cauchy sequence. A Cauchy sequence doesn’t have to converge; some of these sequences in non complete spaces don’t converge at all. Therefore, in order to guarantee convergence it’s important to specify the complete metric space. If you have defined a metric space X, then every convergent sequence in the space V is Cauchy (O’Searcoid, 2010).
- Every real or complex-numbered Cauchy sequence is a bounded sequence,
- If the Cauchy sequence is defined in a metric space and possesses a convergent sub-sequence with a limit, then the sub-sequence is convergent and has the same limit (Porubský, 2008).
The Cauchy Criterion
The Cauchy criterion is a simple theorem that’s very useful when investigating convergence for sequences. Usually, when we check to see if a sequence converges, we have to guess at what the limit should be. The Cauchy criterion, which states that every Cauchy sequence converges, allows us to state that a particular sequence converges without guessing the limit. A very common use of the criterion is the proof that contractive sequences converge [Mendelsohn, 2003].
Despite bearing Cauchy’s name, he surprisingly he made little use of it other than as a version of the completeness property of real numbers [Davis, 2021].
References
Amherst College (2010). Solutions to the Analysis problems on the Comprehensive Examination of January 29, 2010.
Davis, C. (2021). Math 316, Intro to Analysis The Cauchy Criterion. Retrieved May 11, 2021 from: https://people.uwec.edu/daviscw/oldClasses/math316Fall2015/Chapter2/Lecture12/notes.pdf
Gallup, N. (2020). M17 MAT25-21 HOMEWORK 5 SOLUTIONS. Retrieved November 16, 2020 from: https://www.math.ucdavis.edu/~npgallup/m17_mat25/homework/homework_5/m17_mat25_homework_5_solutions.pdf
Goldmakher, L. (2013). Lectures 16 and 17: Summary. Retrieved November 16, 2020 from: https://web.williams.edu/Mathematics/lg5/B43W13/LS16.pdf
Mendelsohn, E. (2003). Transformation and Tradition in the Sciences: Essays in Honour of I Bernard Cohen. Cambridge University Press.
O’Searcoid, M. (2010). Metric Spaces. Springer-Verlag.
Porubský, Š. (2008). Cauchy seq. Retrieved 2020/11/16 from Interactive Information Portal for Algorithmic Mathematics, Institute of Computer Science of the Czech Academy of Sciences, Prague, Czech Republic, web-page http://www.cs.cas.cz/portal/AlgoMath/MathematicalAnalysis/InfiniteSeriesAndProducts/Sequences/CauchySequence.htm