Pearson’s Coefficient of Skewness

Statistics Definitions > Pearson’s Coefficient of Skewness

Click here if you want to find Pearson’s Coefficient of Skewness in Excel.

Watch the video for an example:

see the video? Click here.

What is Pearson’s Coefficient of Skewness?

Karl Pearson developed two methods to find skewness in a sample.

1. Pearson’s Coefficient of Skewness #1 uses the mode. The formula is:
   
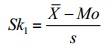
   Where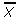 = the mean, Mo = the mode and s = the standard deviation for the sample.
   See: Pearson Mode Skewness.
2. Pearson’s Coefficient of Skewness #2 uses the median. The formula is:
   
   Where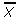 = the mean, Mo = the mode and s = the standard deviation for the sample.
   It is generally used when you don’t know the mode.

Sample problem: Use Pearson’s Coefficient #1 and #2 to find the skewness for data with the following characteristics:

• Mean = 70.5.
• Median = 80.
• Mode = 85.
• Standard deviation = 19.33.

Pearson’s Coefficient of Skewness #1 (Mode):
Step 1: Subtract the mode from the mean: 70.5 – 85 = -14.5.
Step 2: Divide by the standard deviation: -14.5 / 19.33 = -0.75.

Pearson’s Coefficient of Skewness #2 (Median):
Step 1: Subtract the median from the mean: 70.5 – 80 = -9.5.
Step 2: Multiply Step 1 by 3: -9.5(3) = -28.5
Step 2: Divide by the standard deviation: -28.5 / 19.33 = -1.47.

Caution: Pearson’s first coefficient of skewness uses the mode. Therefore, if the mode is made up of too few pieces of data it won’t be a stable measure of central tendency. For example, the mode in both these sets of data is 9:
1 2 3 4 5 6 7 8 9 9.
1 2 3 4 5 6 7 8 9 9 9 9 9 9 9 9 9 9 9 9 10 12 12 13.
In the first set of data, the mode only appears twice. This isn’t a good measure of central tendency so you would be cautioned not to use Pearson’s coefficient of skewness. The second set of data has a more stable set (the mode appears 12 times). Therefore, Pearson’s coefficient of skewness will likely give you a reasonable result.

Interpretation

In general:

• The direction of skewness is given by the sign.
• The coefficient compares the sample distribution with a normal distribution. The larger the value, the larger the distribution differs from a normal distribution.
• A value of zero means no skewness at all.
• A large negative value means the distribution is negatively skewed.
• A large positive value means the distribution is positively skewed.

References

Beyer, W. H. CRC Standard Mathematical Tables, 31st ed. Boca Raton, FL: CRC Press, pp. 536 and 571, 2002.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Lindstrom, D. (2010). Schaum’s Easy Outline of Statistics, Second Edition (Schaum’s Easy Outlines) 2nd Edition. McGraw-Hill Education
“Cook, T. (2005). Introduction to Statistical Methods for Clinical Trials (Chapman & Hall/CRC Texts in Statistical Science) 1st Edition. Chapman and Hall/CRC

---------------------------------------------------------------------------

Need help with a homework or test question? With Chegg Study, you can get step-by-step solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is free!

Comments? Need to post a correction? Please post a comment on our Facebook page.