Hypothesis Testing > How to Calculate the Least significant Difference
How to Calculate the Least Significant Difference (LSD): Overview
Watch the video for an example:
When you run an ANOVA (Analysis of Variance) test and get a significant result, that means at least one of the groups tested differs from the other groups. However, you can’t tell from the ANOVA test which group differs. In order to address this, Fisher developed the least significant difference test in 1935, which is only used when you reject the null hypothesis as a result of your hypothesis test results. The LSD calculates the smallest significant between two means as if a test had been run on those two means (as opposed to all of the groups together). This enables you to make direct comparisons between two means from two individual groups. Any difference larger than the LSD is considered a significant result.
Least Significant Difference (LSD): Formula
The formula for the least significant difference is:
![]()
Where:
- t = critical value from the t-distribution table
- MSw = mean square within, obtained from the results of your ANOVA test
- n = number of scores used to calculate the means.
How to Calculate the Least Significant Difference (LSD): Example Problem
Example problem: Calculate the Least Significant Difference for the difference between two means on Group 1 and Group 2 with the following test results:
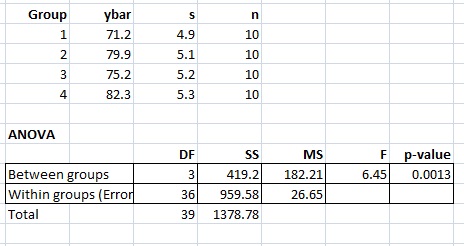
Step 1: Find the t-critical value. The t-critical value for α = 0.05, dfw = 36 is 2.028 (I used the TI-83 calculator to find a t-distribution value). Make sure you are using the Within groups DF from your results!
Step 2: Insert the given values, the MSE from your results (I used 26.65 from Within groups on the above table) the t-distribution value from Step 2 into the least significant difference formula:
- LSD = 2.028 √ (26.65 * (2/10)) = 4.68.
Put this number aside for a moment,
Step 3: Calculate ybar1-ybar2 from the results. For this example, we get -8.7.
Step 4: Compare Step 2 and Step 3. If |ybar1-ybar2| ≥ LSD1,2 then you can reject the null hypothesis that the means are the same (H0:μ1 = μ2).
Our value of 8.7 is larger than 4.68 so we can reject the null hypothesis.
That’s it!
Tip: The LSD will only make sense if you have a significant result from ANOVA (i.e. if you reject the null hypothesis). Therefore, you shouldn’t run the test if you do not get a significant result from ANOVA.
References
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.
Klein, G. (2013). The Cartoon Introduction to Statistics. Hill & Wamg.
Wheelan, C. (2014). Naked Statistics. W. W. Norton & Company