Maximum Volume of Cone Inscribed in a Sphere: Steps
Example question: What is the maximum volume of a cone inscribed inside a sphere with radius r?
Step 1: (Optional) Draw a picture of the problem:
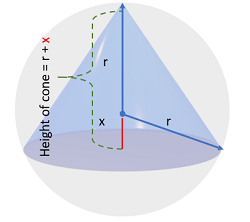
Step 2: Write down the formula for the volume of the cone:
Volume of a cone = ⅓ π R2h
Note that instead of “r” for the radius in this cone formula, I used R. That’s to avoid the confusion of dealing with two radii in this volume problem (one for the cone and one for the sphere).
The next two steps get this expression in terms of one variable, x (so that we can differentiate). Note that “r”, the radius of the sphere, is a constant.
Step 3: Replace the “h” in the cone formula with r + x. Note in the above image that the unknown height of the cone is equal to the radius of the sphere r plus the red segment x
V = ⅓ π R2(r + x)
Step 4: Use the Pythagorean theorem to replace “R” with √(r2 – x2):
V = ⅓ π √(r2 – x2)2(r + x)
Which simplifies to:
V = π/3 (r2 – x2)(r + x)
Expanding (so that we can figure out the derivative in the next step), we get:
V = π/3 (r3 + r2x – rx2 – x3)
Why could we make this substitution? Notice the relationship between R, x and r in the image below:
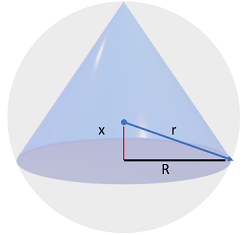
Step 5: Find the Derivative of Step 4. This uses the power rule and the constant rule for derivatives (because “r” is a constant):
![]()
Step 6: Set the derivative equal to zero:
![]()
Step 6: Solve for x:
x = r/3 or x =-r
We can’t have a maximum at “-r”, so the maximum volume happens at x = r/3.
Note: I skipped the algebra steps here, but if you want to see the intermediate steps (like factoring), click here to go to Symbolab’s solver.
Step 7: Insert the value for “x” you found in Step 6 (x = r/3) into the formula you found in Step 4:
- Formula from Step 4: V = π/3 (r2 – x2)(r + x)
- Replacing x with r/3: V = π/3 (r2 – (r/3)2)(r + (r/3))
Solution (click for algebra steps):
The maximum volume of cone inscribed in a sphere is:
![]()
That’s it!