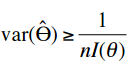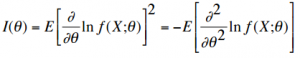Cramer-Rao Lower Bound

Copy

Statistics Definitions > Cramer-Rao Lower Bound

What is the Cramer-Rao Lower Bound?

The Cramer-Rao Lower Bound (CRLB) gives a lower estimate for the variance of an unbiased estimator. Estimators that are close to the CLRB are more unbiased (i.e. more preferable to use) than estimators further away.

The Cramer-Rao Lower bound is theoretical; Sometimes a perfectly unbiased estimator (i.e. one that meets the CRLB) doesn’t exist. Additionally, the CRLB is difficult to calculate unless you have a very simple scenario. Easier, general, alternatives for finding the best estimator do exist. You may want to consider running a more practical alternative for point estimation, like the Method of Moments.

The CLRB can be used for a variety of reasons, including:

  • Creating a benchmark for a best possible measure — against which all other estimators are measured. If you have several estimators to choose from, this can be very useful.
  • Feasibility studies to find out if it’s possible to meet specifications (e.g. sensor usefulness).
  • Can occasionally provide form for MVUE.

Methods

There are a couple of different ways you can calculate the CRLB. The most common form, which uses Fisher information is:

Let X1, X2,…Xn be a random sample with pdf f (x,Θ). If thetahat is an unbiased estimator for Θ, then:
cramer-rao-lower-bound-1


Where:
crlb2


Is the Fisher Information.

You can find examples of hand calculations here.

Calculating the CLRB with Software

At the time of writing, none of the major software packages (like SPSS, SAS or MAPLE) have built in commands for calculating the Cramer-Rao Lower Bound. This download (an unofficial add-in) is available for MATLAB.
Part of the reason for the lack of software is that the CLRB is distribution specific; In other words, different distributions have different tips and tricks to finding it. The computations are outside the scope of this article, but you can find a couple of examples here (for a binomial distribution) and here (for a normal distribution).

Other Names

The Cramer-Rao Lower Bound is also called:

  • Cramer-Rao Bound (CRB),
  • Cramer-Rao inequality,
  • Information inequality,
  • Rao-Cramér Lower Bound and Efficiency.

Comments? Need to post a correction? Please Contact Us.