Contents (Click to skip to that section):
Definition & Formula
Covariance is a measure of how much two random variables vary together. It’s similar to variance, but where variance tells you how a single variable varies, co variance tells you how two variables vary together.
The Covariance Formula
Watch the video for an example:
The formula is:
Cov(X,Y) = Σ E((X – μ) E(Y – ν)) / n-1 where:
- X is a random variable
- E(X) = μ is the expected value (the mean) of the random variable X and
- E(Y) = ν is the expected value (the mean) of the random variable Y
- n = the number of items in the data set.
- Σ summation notation.
Example
Calculate covariance for the following data set:
x: 2.1, 2.5, 3.6, 4.0 (mean = 3.1)
y: 8, 10, 12, 14 (mean = 11)
Substitute the values into the formula and solve:
Cov(X,Y) = ΣE((X-μ)(Y-ν)) / n-1
= (2.1-3.1)(8-11)+(2.5-3.1)(10-11)+(3.6-3.1)(12-11)+(4.0-3.1)(14-11) /(4-1)
= (-1)(-3) + (-0.6)(-1)+(.5)(1)+(0.9)(3) / 3
= 3 + 0.6 + .5 + 2.7 / 3
= 6.8/3
= 2.267
The result is positive, meaning that the variables are positively related.
Note on dividing by n or n-1:
When dealing with samples, there are n-1 terms that have the freedom to vary (see: Degrees of Freedom). We only know sample means for both variables, so we use n – 1 to make the estimator unbiased. for very large samples, n and n – 1 would be roughly equal (i.e., for very large samples, we would approach the population mean).
Back to top
Problems with Interpretation
A large covariance can mean a strong relationship between variables. However, you can’t compare variances over data sets with different scales (like pounds and inches). A weak covariance in one data set may be a strong one in a different data set with different scales.
The main problem with interpretation is that the wide range of results that it takes on makes it hard to interpret. For example, your data set could return a value of 3, or 3,000. This wide range of values is cause by a simple fact; The larger the X and Y values, the larger the covariance. A value of 300 tells us that the variables are correlated, but unlike the correlation coefficient, that number doesn’t tell us exactly how strong that relationship is. The problem can be fixed by dividing the covariance by the standard deviation to get the correlation coefficient.
Corr(X,Y) = Cov(X,Y) / σXσY
Back to top
Advantages of the Correlation Coefficient
The Correlation Coefficient has several advantages over covariance for determining strengths of relationships:
- Covariance can take on practically any number while a correlation is limited: -1 to +1.
- Because of it’s numerical limitations, correlation is more useful for determining how strong the relationship is between the two variables.
- Correlation does not have units. Covariance always has units
- Correlation isn’t affected by changes in the center (i.e. mean) or scale of the variables
Calculate Covariance in Excel
Watch the video or follow the steps below (this is for Excel 2013, but the steps are the same for Excel 2016):
Covariance in Excel: Overview
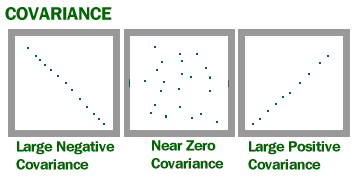
Covariance gives you a positive number if the variables are positively related. You’ll get a negative number if they are negatively related. A high covariance basically indicates there is a strong relationship between the variables. A low value means there is a weak relationship.
Covariance in Excel: Steps
Step 1: Enter your data into two columns in Excel. For example, type your X values into column A and your Y values into column B.
Step 2: Click the “Data” tab and then click “Data analysis.” The Data Analysis window will open.
Step 3: Choose “Covariance” and then click “OK.”
Step 4: Click “Input Range” and then select all of your data. Include column headers if you have them.
Step 5: Click the “Labels in First Row” check box if you have included column headers in your data selection.
Step 6: Select “Output Range” and then select an area on the worksheet. A good place to select is an area just to the right of your data set.
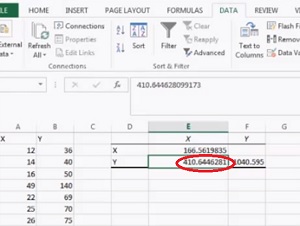
Step 7: Click “OK.” The covariance will appear in the area you selected in Step 5.
That’s it!
Tip: Run the correlation function in Excel after you run covariance in Excel 2013. Correlation will give you a value for the relationship. 1 is perfect correlation and 0 is no correlation. All you can really tell from covariance is if there is a positive or negative relationship.
Check out our YouTube channel for more Excel tips and help!
References
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.