Hypothesis Testing > Welch’s ANOVA
What is Welch’s ANOVA?
Welch’s ANOVA compares two means to see if they are equal. It is an alternative to the Classic ANOVA and can be used even if your data violates the assumption of homogeneity of variances.
You should run Welch’s test in all cases where you have normally distributed data that violates the assumption of homogeneity of variance. ANOVA (and the non-parametric alternative Kruskal-Wallis) are very unstable for these situations, producing Type I error rates that are:
- Conservative for large sample sizes and
- Inflated for small sample size.
Welch’s ANOVA is fast becoming the go-to method out of the three. For normal, different-variance, and balanced data (i.e. same-size samples), Welch’s has the most power and the lowest type I error rate. However, classic ANOVA still performs the best when data is normal, equal-variance, and is either balanced or unbalanced. In other words, run Welch’s if your data has unequal variances, but run a classic ANOVA if it’s just an unequal sample size issue.
How to Run Welch’s ANOVA
The assumptions are pretty much the same for Welch’s ANOVA as for the classic ANOVA. For example, the assumption of normality still holds. However, you should run Welch’s when you violate the assumption of equal variances. You can run it with unequal sample sizes.
In Minitab: the Assistant automatically runs Welch’s when you choose an ANOVA test. You can also run it by clicking “ANOVA > One-Way”, then clicking “Options” and unchecking “Assume equal variances.”
In SAS: Add a MEANS statement, the nominal variable name, and then type a slash followed by “WELCH”. For example:
PROC anova;
CLASS A B;
MODEL Y=A B;
MEANS AB / WELCH;
RUN;
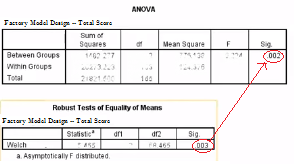
In SPSS, click “Analyze > Compare Means > One-Way ANOVA”. Then click “Options” and check both the “Homogeneity of variance” test and the “Welch” box. This will test for homogeneity of variance and then — if the assumption is violated — you can use the Welch statistic (otherwise you can choose to use Sig. in the regular ANOVA output instead of the Sig. reported in the Welch area).
References:
Moder, K. (2007). How to keep the Type I Error Rate in ANOVA if Variances are
Heteroscedastic. Austrian Journal of Statistics, 36(3), 179-188.
Moder, K. (2010). Alternatives to F-Test in One Way ANOVA in case of heterogeneity
ofvariances (a simulation study). Psychological Test and Assessment Modeling, Volume 52,
2010 (4), 343-353
Vogt, W.P. (2005). Dictionary of Statistics & Methodology: A Nontechnical Guide for the Social Sciences. SAGE.