Asymptotic Error (Rate of Convergence)

Sequence and Series >

Contents:

• What is the Asymptotic Error Constant?
• Order of Convergence

What is the Asymptotic Error Constant?

The asymptotic error constant (λ) tells you something about the behavior of a sequence’s errors: differences between the terms of the sequence and the sequence’s limit. The asymptotic error constant affects the speed of convergence in conjunction with the order of convergence.

How to Find the Asymptotic Error Constant

You can find a sequence’s asymptotic error constant λ with the following limit definition:


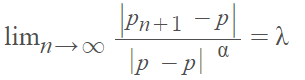
Where:

• α = order of convergence,
• p_n = a sequence,
• p = where the sequence converges (p_n ≠ p).

As the number of terms increases, the sequence approaches the limit or horizontal asymptote; λ tells you the rate at which that happens. If positive constants λ and α exist for the above limit, then the sequence converges to p of order of α at rate λ.

In general, a sequence with a higher order of convergence will converge faster than a sequence with a lower order of convergence (the asymptotic constant also affects the speed of convergence, but not to the extent that the order does)[1]:

• If α = 1, p_n converges to p linearly.
• If α = 2, p_n converges to p quadratically.
• If α = 3, p_n converges to p cubically.
• If 0 < α < 1, p_n converges to p suberlinearly.
• If 1 < α < 2, p_n converges to p superlinearly.

While there are many possible values for order of convergence, most of the sequences you’ll come across in beginning calculus and analysis classes will have α = 1 or α = 2.

For example, the following two sequences both converge to 5:


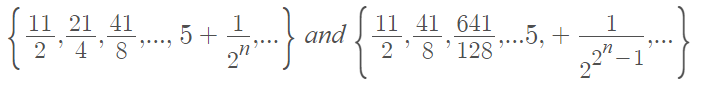
However, they converge with different orders of convergence.

The first sequence converges linearly (α = 1) to 5:

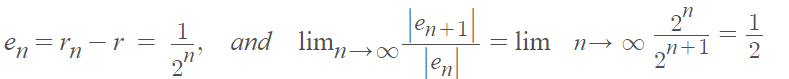
The second sequence converges quadratically (α = 2) to 5:

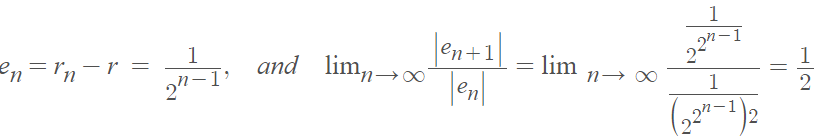
Asymptotic Error Constant: Example

Example question: What is the asymptotic error constant for the sequence:

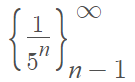
Step 1: Find the limit of the sequence:



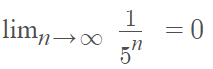
For this sequence, p = 0.

Step 2: Insert p from Step 1 and α from Step 2 into the formula and solve. Using the definition of the asymptotic error constant, the sequence has order of convergence α if λ exists in the limit and is finite. This particular sequence converges linearly (α = 1):

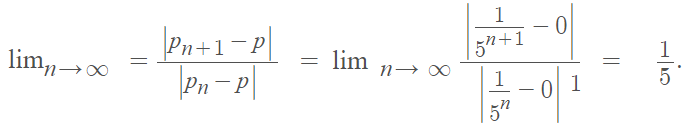
Order of Convergence

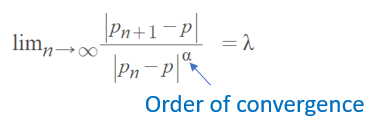
The order of convergence α affects how fast a sequence converges to its limit. It’s used in conjunction with the asymptotic error constant.

Larger values of α converge faster. For example:

• If 0 < α < 1, a sequence is suberlinearly convergent to p.
• If α = 1 (and λ < 1), a sequence is linearly convergent to p.
• If 1 < α < 2, a sequence is superlinearly convergent to p.
• If α = 2, a sequence is quadratically convergent to p.
• If α = 3, a sequence is cubically convergent to p.

If a sequence has a higher order of convergence, fewer iterations are needed to give a useful approximation.

Order of convergence looks at the relationship between successive error values. Basically, it measures the effectiveness of reducing the approximation error with each iteration. Big O notation is similar, but and gives the rate of convergence; It’s not sufficient to describe how fast the convergence is. For sequences that converge quickly, order of convergence is usually much better at describing speed of convergence [1].

References

[1] Order of Convergence. Retrieved November 30, 2021 from: https://arnold.hosted.uark.edu/NA/Pages/OrderConv.pdf
Chapter 2: Solutions of Equations in One Variable. Retrieved August 14, 2021 from: https://www.math.tamu.edu/~smpun/MATH417/Chapter-2.pdf