Statistics Definitions > Variance Inflation Factor
You may want to read this article first: What is Multicollinearity?
What is a Variance Inflation Factor?
A variance inflation factor(VIF) detects multicollinearity in regression analysis. Multicollinearity is when there’s correlation between predictors (i.e. independent variables) in a model; its presence can adversely affect your regression results. The VIF estimates how much the variance of a regression coefficient is inflated due to multicollinearity in the model.
VIFs are usually calculated by software, as part of regression analysis. You’ll see a VIF column as part of the output. VIFs are calculated by taking a predictor, and regressing it against every other predictor in the model. This gives you the R-squared values, which can then be plugged into the VIF formula. “i” is the predictor you’re looking at (e.g. x1 or x2):
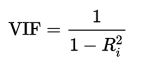
Interpreting the Variance Inflation Factor
Variance inflation factors range from 1 upwards. The numerical value for VIF tells you (in decimal form) what percentage the variance (i.e. the standard error squared) is inflated for each coefficient. For example, a VIF of 1.9 tells you that the variance of a particular coefficient is 90% bigger than what you would expect if there was no multicollinearity — if there was no correlation with other predictors.
A rule of thumb for interpreting the variance inflation factor:
- 1 = not correlated.
- Between 1 and 5 = moderately correlated.
- Greater than 5 = highly correlated.
Exactly how large a VIF has to be before it causes issues is a subject of debate. What is known is that the more your VIF increases, the less reliable your regression results are going to be. In general, a VIF above 10 indicates high correlation and is cause for concern. Some authors suggest a more conservative level of 2.5 or above.
Sometimes a high VIF is no cause for concern at all. For example, you can get a high VIF by including products or powers from other variables in your regression, like x and x2. If you have high VIFs for dummy variables representing nominal variables with three or more categories, those are usually not a problem.
References
Dodge, Y. (2008). The Concise Encyclopedia of Statistics. Springer.
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.