Transfinite numbers are infinite…but not quite. They are either cardinal numbers or ordinal numbers, and are used to compare the sizes of infinite sets.
While it might seem that one infinite set should be the same size as another (i.e. they are both “infinite”), a comparison of some sets suggests that one set of infinite numbers is actually larger than another. For example, the set of integers (1, 2, 3…) is a subset of rational numbers (which include 1, 2, 3… plus any fraction like 1/2, 1/3 etc.). Therefore, the set of rational numbers should, in theory, be larger.
Understanding Transfinite Numbers
The cardinality of a finite set tells us the size of the set (i.e. how many elements it has). For example, the cardinality of the set {0, 1, 2, 3} is four, and the cardinality of the set {1} is just one. There is just one empty set, {}, with a cardinality of zero.
The set of natural numbers has infinite cardinality. It goes on further than you can count, and has no end; There are an infinite number of elements in it. What about integers? They have the natural numbers as a subset, but you could also pair them with the set of natural numbers, and count them off that way. Therefore, they have the same cardinality. This is called countable, and as a cardinal transfinite number it is represented by aleph-naught, ℵ0 , the Hebrew letter aleph with a 0 subscript.
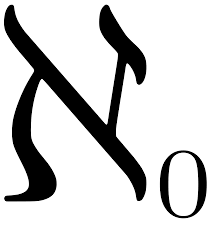
But what about the real numbers? There are even more of them; Cantor proved that there couldn’t be a one-to-one pairing with the natural numbers. This is a bigger infinity. It is sometimes called c, but as a cardinal number is also referred to as ℵ1 . That’s because it’s been shown to be the next biggest transfinite number after ℵ 0 . There are no sets with cardinality between ℵ 0 and ℵ 1 .
History
The theory of transfinite numbers was developed by mathematician Georg Cantor, who lived between 1845 and 1918 and is known as the father of set theory. Before Cantor began his work, infinity was thought of as a single, absolute concept; your infinity could not be bigger than mine, for example. But Cantor’s study of the cardinality of sets contradicted that idea.
References
Srivastava, S M. Transfinite Numbers: What is Infinity? Retrieved from https://www.ias.ac.in/article/fulltext/reso/002/03/0058-0068 on June 16, 2019