An open unit disk (sometimes just called the unit disk) just means a disc with a radius of one. That’s the inside of the unit circle, or the region in the plane that centered around a given point. It can be defined as
![]()
Here, P is the given point in the plane (that we’re centering around). This definition works equally well in the Euclidean plane or complex plane.
If no specifications are given, an open unit disk can be assumed to be the interior of a circle of radius 1 which is centered about the origin. The disk is defined as the region {z: |z| < 1}, where |z| is the complex modulus.
Examples of Open Unit Disk
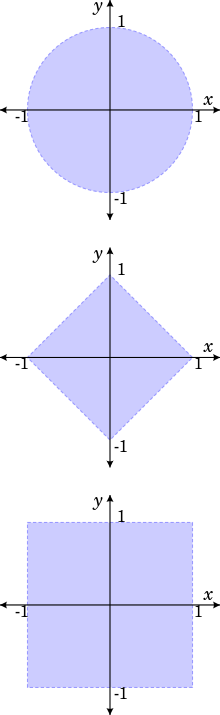
The basic definition of an open unit disk, given above, is relatively simple. But that doesn’t mean that it always has to look like that; It isn’t always a nice, neat circle centered around an obvious axis. In fact, in other metrics the open unit disk doesn’t even look like a disk at all.
In both the taxicab metric and Chebyshev metric, unit disks look like squares. Their topology and most of their properties are the same as Euclidean unit disks; they just look different. One property though that is not the same is their area.
In a Euclidean metric, a radius of 1 means that the area of the unit disk is π and perimeter 2pi;. In taxicab metric, though, the perimeter of the unit disk is 8. It has been shown that if we consider all metrics which arise from a norm, the perimeter of the unit disk may be anything from 6 to 8 but cannot deviate from that.
Note on the Chebyshev Distance
Given two vectors or points p and q, with standard coordinates pi and qi, the Chebyshev distance is, respectively: DChebyshev(p, q) := maxi (|pi – qi|). See: Distances in classification.
References
Cafe Scientifique. Distances in Classification. Retrieved December 16, 2019 from: http://www.ieee.ma/uaesb/pdf/distances-in-classification.pdf
Gross and Yellen. Graph Theory and Its Applications. Section 8.1: The Topology of Low Dimensions. Retrieved from https://books.google.com/books?id=-7Q_POGh-2cC on November 24, 2019.