Summability theory , which began in the 19th century, is part of analysis (the branch of mathematics dealing with limits and related theories). It generalizes the concept of convergence to all sequences—even nonconvergent ones. It attempts to create an algorithm that assigns a limit to nonconvergent sequences; The theory makes a nonconvergent series converge, in a general sense, whenever a sequence of positive linear operators doesn’t ordinarily converge.
Although matrices can be used as a summability method, matrices are not required.
Applications include [1]:
- Fejer’s theorem on convergence of Fourier series,
- Komlos’ theorem for L1-bounded sequences,
- The weak and strong laws of large numbers.
Types
Summability methods can be assigned to a certain type [2]:
- Regular: The algorithm sums all convergent series to its Cauchy sum.
- Consistent: Two methods are consistent if they cannot sum the same series to different sums.
- Stronger: One summability method A is “stronger” than another method B if summability of a series by B implies its summability by A.
Summability Theory Example: Cesaro Method
A series a1 + a2 + … converges to the sum s if the sequence of partial sums s1 + s2 + … approach the limit s. The Cesaro method defines another sequence, t1 + t2 + …, where each term is the mean of the first n terms in the sequence of partial sums. If tn → s as n → &infin, then the series a1 + a2 + … is Cesaro summable to s [3].
For a sequence of real- or complex-valued terms a1, a2, …, a3, the Cesaro method is defined as [4]:
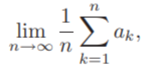
provided the limit exists. The method gives the correct solution for convergent sequences and many nonconvergent ones. For example, it gives the correct limit of zero for ak = (−1)k. However, there are several nonconvergent ones for which the algorithm doesn’t work.
References
[1] Cakalli, H. & Khan, M. (2010). Summability in Topological Spaces. Retrieved July 5, 2021 from: http://www.math.kent.edu/~kazim/NorthFloridaU/NorthFlor.pdf
[2] Samanta, P. (2016). Introduction to Summability Theory. Retrieved July 5, 2021 from: https://www.researchgate.net/publication/318027036_Introduction_to_Summability_Theory
[3] Roberts, K. (2010). What is Summability Theory? Retrieved July 5, 2021 from: https://publish.uwo.ca/~krobe8/what-sum-thy.pdf
[4] Khan, K. (2011). Summer Workshop on Distribution Theory & its Summability Perspective.