What is an Attracting Fixed Point?
A fixed point is a point where f(x) = x. In other words, it’s the set of points for the graph of f that cross the diagonal y = x.
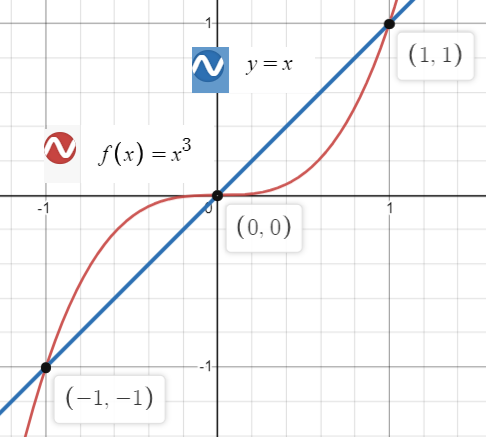
An attracting fixed point is a fixed point that “attracts” the numbers surrounding it: if we start with a number sufficiently close to x , iterating it will always result in convergence to x. A repelling fixed point shows the opposite behavior: it pushes the nearby numbers away. These facts can be described by the behavior of the derivative of the fixed point [1]:
- If the absolute value of the derivative is less than 1, the point is attracting.
- If the absolute value of the derivative is greater than 1, the point is repelling.
Orbits and Periodic Points
The forward orbit (or simply orbit) of a point (called the seed or initial point of the orbit) is the set of places where the point can be moved by group action.
More formally, the orbit of point x0 under F is defined as the sequence x0, x0, x1, x2,… where xn + 1 = F(xn) for n ≥ 0.
As an example, let’s say we have a real-valued function f(x) = √x.
If x0 = 256 then x1 = √256 = 16, x2 = √16 = 4; and so on. The next few terms in the orbit are 2, 1.414213562, 1.189207115, 1.090507733, 1.044273783 [2].
Within a dynamical system, there are many orbit types. The orbit of a fixed point is the constant sequence x0, x0, x0, … [3]. Periodic orbits are solutions to dynamical systems that repeat over time. Periodic orbits, like fixed points, can also be attracting, repelling, or neutral [4]:
- Attracting periodic orbit: orbits of nearby points converge to the periodic orbit,
- Repelling periodic orbit: orbits of nearby points move away from the periodic orbit,
- Neutral periodic orbit: orbits of nearby points neither converge to nor move away from the periodic orbit.
Attracting Fixed Point and the Basin of Attraction
If x0 is an attracting fixed point for a function f, then the basin of attraction for x0 is the set of all points with orbits tending to x0 [5]. The immediate basin of attraction is the largest interval in the basin that contains x0.
References
[1] Seidel, P. (2011). Iteration, Fixed Points. Retrieved July 7, 2021 from: https://math.mit.edu/classes/18.01/F2011/lecture3.pdf
[2]
[3] Mace, K. Chaos and Dynamics. Retrieved July 7, 2021 from: https://www.whitman.edu/Documents/Academics/Mathematics/macemk.pdf
[4] Osinga, H. (1998). One-Dimensional Dynamical Systems: Part 4: Linear and Nonlinear Behavior. Retrieved July 7, 2021 from: http://www.geom.uiuc.edu/~math5337/ds/part4/part4_per.html
[5] McKinney, W. (2005). The Schwarzian Derivative & the Critical Orbit. Retrieved July 7, 2021 from: https://ocw.mit.edu/courses/mathematics/18-091-mathematical-exposition-spring-2005/lecture-notes/lecture09.pdf