Finite Geometric Sequence

Sequence and Series >

A finite geometric sequence is a list of numbers (terms) with an ending; each term is multiplied by the same amount (called a common ratio) to get the next term in the sequence.
For example: the sequence 5, 10, 20, 40, 80, … 320 ends at 320. Each term is multiplied by 2 to get the next term.

Note: A slightly different form is the geometric series, where terms are added instead of listed: a + ar + ar² + ar³ + …. These behave differently, and their sums are different. This article is about the geometric sequence; If you want to learn about the series, see: What is a Geometric Series?

Nth Term of a Geometric Sequence

The general form of the sequence is a₁,  a₁r₂,   a₁r₃,   a₁r₄,…  a₁r_{(n – 1)}
.We don’t always want to write out the entire sequence all the time, so instead of writing everything out (5, 10, 20, 40, 80, 160…) we can use a much shorter formula. The general formula for the nth term of a geometric sequence is:

a_n = a₁r^{(n – 1)}

Where:

• a₁ = the first term in the sequence,
• r = the common ratio.
• n = the nth term.

For the example sequence above, the common ratio is 2 and the first term is 5. We can find out the nth terms by plugging those into the formula:
a_n = 5 · 2^{(n – 1)}.

• First term: 5 · 2^{(1 – 1)} = 5 · 2⁽⁰⁾ = 5 · 1 = 5
• Second term: 5 · 2^{(2 – 1)} = 5 · 2⁽¹⁾ = 5 · 2 = 10
• Third term: 5 · 2^{(3 – 1)} = 5 · 2⁽²⁾ = 5 · 4 = 20
• Fourth term: 5 · 2^{(4 – 1)} = 5 · 2⁽³⁾ = 5 · 8 = 40

Another example: let’s say you are given 6(3)^{n – 1} and you’re asked to find the first five terms. Note: The first term in the formula is always in the first position, you know the first term here is 6.

• First term: 6
• Second term: 6 · 3^{2 – 1} = 6 · 3¹ = 18
• Third term: 6 · 3^{3 – 1} = 6 · 3 ² = 54
• Fourth term: 6 · 3^{4 – 1} = 6 · 3 ³ = 162
• Fifth term: 6 · 3^{5 – 1} = 6 · 3 ⁴ = 486

Sum of a Finite Geometric Sequence

The sum of a finite geometric sequence is given by the formula (Larson, 2014):

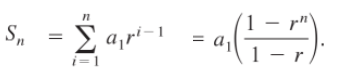
Where:

• r = common ratio (r ≠ 1),
• Σ = sigma notation (“add everything up”)

Example question: What is the sum of the first 7 terms of a finite geometric series if the first term (a₁ = 1 and the common ratio (r) = 2?

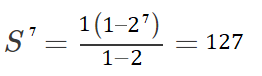
References

Harrison, B. (2020). Take Your Medicine. Adapted from Section 9.1 in Hughes-Hawlett, Deborah, et.al; Single Variable Calculus; John Wiley & Sons, Inc.; New York; 2002
Larson, R. (2014). College Algebra. Cengage Learning.
Seward, K. (2011). College Algebra: Tutorial 54D: Geometric Sequences and Series. Retrieved August 24, 2020 from: https://www.wtamu.edu/academic/anns/mps/math/mathlab/col_algebra/col_alg_tut54d_geom.htm