Statistics Definitions > Relative Standard Deviation
What is a Relative Standard Deviation?
Watch the video for an example of how to find the relative standard deviation:
The relative standard deviation (RSD) is a special form of the standard deviation (std dev).
You may want to read this previous article first:
How to find Standard Deviation
The relative standard deviation formula is:
100 * s / |x̄|
Where:
s = the sample standard deviation
x̄ = sample mean
It’s generally reported to two decimal places (i.e. an RSD of 2.9587878 becomes 2.96). As the denominator is the absolute value of the mean, the RSD will always be positive.
The RSD tells you whether the “regular” std dev is a small or large quantity when compared to the mean for the data set. For example, you might find in an experiment that the std dev is 0.1 and your mean is 4.4. Your RSD for this set of numbers is:
100 x 0.1 / |4.4| = 2.3%.
This result tells you that your standard deviation is 2.3% of the mean of 4.4, which is pretty small. In other words, the data is tightly clustered around the mean. On the other hand, if your percentage was large, say, 55%–this would indicate your data is more spread out. The RSD is sometimes used for convenience but it can also give you an idea about how precise your data is in an experiment. The more precise your data, the smaller the RSD.
The RSD usually written with the mean and a plus/minus symbol:
4.4 ± 2.3%.
How to Calculate the Relative Standard Deviation (Steps)
Sample question: Find the RSD for the following set of numbers:
49, 51.3, 52.7. 55.8
Step 1: Find the standard deviation of your sample. I used the standard deviation calculator to solve this. Std dev: 2.8437065 (or 2.84 rounded to 2 decimal places).
Step 2: Multiply Step 1 by 100. Set this number aside for a moment.
2.84 * 100 = 284
Step 3: Find the sample mean, x̄. The sample mean is:
(49 + 51.3 + 52.7 + 55.8) / 4 = 208.8/4 = 52.2.
Step 4: Divide Step 2 by the absolute value of Step 3.
284/|52.2| = 5.44
The RSD is:
52.2 ±5.4%
Note that the RSD is expressed as a percentage.
Relative Standard Deviation Excel
There isn’t a built in function” rel=”noopener” target=”_blank”>function to find the RSD in Excel. Use a combination of the following commands to get the mean and std dev, then multiply by 100:
- =average(a1:A10)
- =std dev(a1:A10)
For example, assuming the mean is in cell B1 and the std dev is in cell B2, you could type in cell B:
=(b2/b1)*100
If the result is negative, just take the absolute value to make it a positive number.
Relative Standard Deviation and Coefficient of Variation
In some cases, the coefficient of variation and the RSD are the same thing. However, the RSD cannot be negative while the Coefficient of Variation can be positive or negative. This is because the two formulas differ in a minor way: the Coefficient of Variation divides by the mean while the RSD divides by the absolute value of the mean.
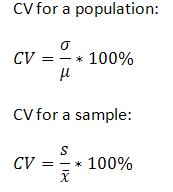
Above: Coefficient of variation formulas.
Check out our statistics YouTube channel for hundreds of videos on elementary stats.
References
Everitt, B. S.; Skrondal, A. (2010), The Cambridge Dictionary of Statistics, Cambridge University Press.
Gonick, L. (1993). The Cartoon Guide to Statistics. HarperPerennial.